Teorema lui Thales - Formula și definiție

Matematica este un domeniu care îi fascinează pe mulți. Încă din antichitate, numeroși oameni de știință au încercat să îi dezlege tainele și să afle ce se ascunde în spatele cifrelor și a diverselor forme geometrice.

Un nume care s-a remarcat în acest sens a fost și Thales, care a descoperit o teoremă conform căreia o paralelă la una dintre laturile unui triunghi determină segmente proporționale pe celelalte două laturi.

Înainte însă de a-ți explica mai multe și de a te ajuta să înțelegi această teoremă vrem să îți vorbim puțin despre cine a fost Thales și cum a ajuns să facă descoperiri atât de importante.

Cine a fost Thales

Thales din Milet a fost un filozof grec, născut în jur de 626-623 î. Hr., în Milet, Ionia, Turcia, din strămoși cu origini feniciene. Părinții lui au fost Examyes și Cleobulina, despre care nu se știu prea multe date.

Nu există informații despre copilăria și educația timpurie a lui Thales, însă, conform The Collector, se crede că ar fi fost școlit în Egipt și Babilon, ceea ce l-a ajutat să se dezvolte și să fie tot mai interesat de lumea matematicii și nu numai. Se pare că civilizațiil din aceste zone l-au influențat într-un mod profund și l-au dezvoltat din punct de vedere intelectual.

Considerat de mulți ca fiind părintele filozofiei occidentale, Thales a fost fondatorul filosofiei grecești și implicit a Școlii Milesiene a Cosmologiștilor. Ceea ce acesta a vrut să facă și i-a și reușit a fost să lase la o parte miturile legate de intervențiile zeilor și să demonstreze lumea naturală prin rațiune, cu ajutorul gândirii științifice.

În epoca în care a trăit, Thales era foarte bine văzut, fiind perceput ca un om inteligent, cu o serie de capacități uimitoare. Era nominalizat în toate listele cu înțelepți, își punea diverse întrebări despre univers și apoi le împărtășea cu lumea tot ce afla.

Modul în care marele filozof a murit este unul destul de rar întâlnit. Se pare că și-a găsit sfârșitul în timpul unor manifestații sportive, în anii 540 î. Hr., la vârsta de 80 ani, din cauza căldurii.

Inscripția de pe mormântul să amintește și ea de cât de mare a fost și de interesul său pentru univers „Aici, într-un mormânt strâmt, zace marele Thales; totuşi renumita sa înțelepciune a ajuns la ceruri”.

Ce demonstrații a făcut Thales de-a lungul timpului

Din cauza faptului că nu s-au păstrat scrierile lui Thales, au tot existat dubii în privința celor demonstrate de el. Cu toate acestea, W i kipedia ne spune că filozofi precum Proclus sau Diogenes, i-au atribuit descoperiri precum:

diametrul împarte cercul în două părți egale;
unghiurile bazei unui triunghi isoscel sunt congruente;
unghiurile care sunt opuse la vârf sunt congruente;
o latură și unghiurile adiacente ei pot determina un triunghi;
unghiul care este înscris într-un semicerc este un unghi drept;
o paralelă dusă la una dintre laturile unui triunghi formează segmente proporționale pe celelalte două laturi ale triunghiului dat (cunoscută sub numele de Teorema lui Thales).

Descoperirile făcute de Thales au fost de-a lungul timpului disponibile unor mari filozofi precum: Aristotel, Platon sau Heraclitus.

Cum a descoperit Thales teorema care îi poartă numele

Dacă ai o curiozitate legată de cum a descoperit Thales teorema care îi poartă numele, ei bine, nu se știe exact modul în care el a procedat pentru a ajunge la această concluzie.

Cel mai probabil, în călătoriile sale a observat tot felul de tehnici utilizate pentru măsurători și încetul cu încetul a reușit să își dea seama de faptul că dacă trasezi o linie paralelă la o latură a unui triunghi, întotdeauna obții segmente proporționale.

Cum și-a demonstrat Thales teorema

În cartea „Istoria matematicii”, de Carl B. Boyer, autorul spune că dovezi clare în privința modului în care Thales și-a demonstrat teoremele nu există, și că primele dovezi cu adevărat puternice au apărut abia la Euclid.

Howard Eves, un matematician american a fost de părere că Thales a folosit metode mai puțin formale pentru a-și demonstra teoriile. Iată câteva dintre ele:

observație directă și experimentală – ceea ce ar fi putut face Thales ar fi fost să traseze în mod repetat linii paralele cu latura unui triunghi și să observe că de fiecare dată raporturile de segmente erau identice.
raționament intuitiv și analogic – aici putem vorbi despre influența tehnicilor de măsurare pe care Thales le-a văzut la civilizațiile egiptene și babiloniene.
geometrie aplicată – în acest caz cel mai probabil Thales a încercat să aplice cunoștințele de geometrie pe care le avea la acel moment.

Dacă a avut sau nu Thales o demonstrație scrisă la cele spuse, nu putem ști, însă, se pare că el a fost cel care a sesizat și a exprimat pentru prima dată această idee.

Termeni importanți în teorema lui Thales

Pentru a-ți fi mai ușor să înțelegi teorema lui Thales, este important să știi exact la ce se referă anumiți termeni folosiți în definiția ei:

linie paralelă – o linie paralelă este o dreaptă care indiferent de cât ar fi prelungită nu se va intersecta cu o altă dreaptă;
triunghi – un triunghi este o formă geometrică formată din trei puncte care se unesc în trei segmente și care duc la formarea a trei unghiuri;
segmente proporționale – acestea sunt segmente care își păstrează același raport între lungimile lor;
similitudine – acest termen face referire la proprietatea a două figuri geometrice de a-și păstra forma atunci când au dimensiuni diferite.

Teorema lui Thales – ce este și ce formulă are

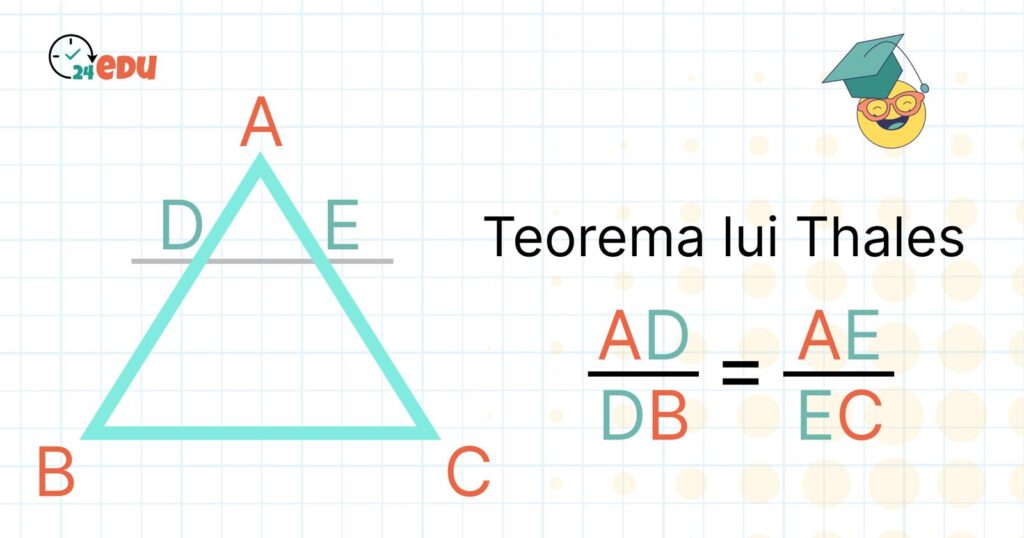
Teorema lui Thales, așa cum am spus și mai sus, este o teoremă care stabilește faptul că o dreaptă paralelă care este trasată din una din laturile unui triunghi va determina segmente proporționale pe celelalte două laturi ale triunghiului.

Fiind vorba de matematică, această teoremă are și o formulă pe care vrem să ți-o explicăm puțin.

avem un triunghi ABC;
avem o dreaptă paralelă cu latura BC;
dreapta paralelă BC intersectează latura AB în punctul D;
dreapta paralelă BC intersectează latura AC în punctul E.

Acestea fiind zise, se va forma un raport care va respecta următoarele date:

Dacă te interesează un exemplu cu cifre, pentru a înțelege mai bine, se dau următoarele date:

AD = 3 cm;
DB = 6 cm;
AE = 4 cm.

Raportul dintre AD și DB este de 3/6, adică 0.5. Pentru a-l păstra, avem segmentul AE = 4 cm, iar EC va fi dublu, adică 8 cm. Astfel, vor rezulta următoarele:

Teorema pe care o enunță Thales se bazează pe principiul triunghiurilor similare, ceea ce înseamnă că triunghiul mare ABC va fi similar cu triunghiul mic ADE, deoarece acestea au unghiurile comune – cel din vârful A și cele două formate la intersecția dintre laturile AB și AC cu dreapta paralele DE.

Ce s-a aflat de-a lungul timpului cu ajutorul teoremei lui Thales

Chiar dacă pentru unii această teoremă ar putea fi destul de dificil de înțeles, în practică, prin intermediul ei s-au reușit de-a lungul timpului să se facă o serie de măsurători, dar și să se dezvolte diverse concepte:

măsurarea înălțimilor – în cartea sa An Introduction to the History of Mathematics, autorul Howard Eves spune că una dintre cele mai notabile măsurători făcute cu ajutorul teoremei lui Thales a fost cea a piramidelor din Egipt. Aceasta s-a făcut pe baza proiecției umbrelor și a segmentelor proporționale date ele. Acest lucru îl consemnează și matematicianul Carl B. Boyer în Istoria matematicii.
geometria euclidiană – Euclid s-a folosit de teorema lui Thales pentru a pune bazele conceptului de triunghiuri similare și teoria proporționalității, așa cum se găsește în consemnele sale făcute în cartea Elementele.
topografie și cartografie – în aceste domenii teorema lui Thales a fost de mare ajutor, deoarece cu ajutorul ei s-a reușit măsurarea cu precizie a terenurilor, dar și realizarea de hărți. Chiar și astăzi sunt ingineri care încă se mai folosesc de teorema lui Thales în măsurătorile pe care le fac.
astronomie – cu ajutorul acestei teoreme atât de cunoscute de oamenii de știință, s-a reușit în antichitate să se măsoare chiar și înălțimea stelelor.
navigație – în domeniul navigației antice, teorema lui Thales a fost folosită la acele vremuri pentru a afla poziția pe care o aveau diverse nave, dar și distanțe pe mare.

E uimitor cât de multe lucruri s-au putut afla cu ajutorul acestei teoreme. Astăzi, datorită tehnologiei moderne, toate aceste măsurători sunt mult mai ușor de făcut, dar să nu uităm că la baza lor a stat mult studiu și multă muncă.

De ce este Teorema lui Thales importantă în domeniul matematicii

Teorema lui Thales a pus bazele matematicii moderne, motiv pentru care este de o importanță covârșitoare. Thales a fost cel care a făcut pentru prima dată o serie de afirmații logice, lăsând la o parte ceea ce se făcea până atunci, și anume observațiile empirice.

Teorema lui Thales a ajutat foarte mult la dezvoltarea geometriei demonstrative, așa cum specifică și matematicieni precum Carl B. Boyer sau Howard Eves în cărțile lor.

Totodată, teorema lui Thales este considerată a fi baza teoriei triunghiurilor similare, ceea ce a ajutat la stabilirea clară a unor raporturi și proporții geometrice, aspecte deosebit de importante în trigonometrie și geometrie proiectivă.

În ce domenii poate fi folosită în practică Teorema lui Thales

Teorema lui Thales este mult mai practică decât ar putea crede unii la o primă vedere. Sunt nenumărate domenii în care ea poate fi aplicată cu succes:

topografie și geodezie – pentru a măsura distanțele de pe suprafețe mai greu accesibile, dar și pentru a determina limitele unor terenuri sau pentru a ajuta la crearea de hărți;
construcții și arhitectură – de mare ajutor când vorbim de măsurarea înălțimii clădirilor, turnurilor sau a diverselor alte structuri, dar și pentru a planifica proporțiile în construcții sau pentru a verifica corectitudinea proiectelor;
navigație – pentru a calcula distanțe maritime utilizând anumite puncte de reper, dar și pentru a calcula poziția navelor;
astronomie – a permis calcularea distanțelor și înălțimilor corpurilor cerești față de orizont, dar și poziția planetelor și a stelelor;
inginerie mecanică și proiectare – pentru a menține proporții precise în componentele mecanice, dar și pentru a scala modele.
fotografie – de ajutor pentru calculul distanțelor focale și a unghiurilor.

Din câte poți observa, în practică, teorema lui Thales este foarte utilizată și rămâne de mare importanță și actualitate și astăzi, după mii de ani.

Cum pot învăța elevii Teorema lui Thales

Pentru elevi poate fi destul de dificil de înțeles această teoremă, însă, vom încerca să îți dăm câteva idei care ar putea să funcționeze:

învățarea prin exemple concrete

Nimic nu poate ajuta mai mult un elev să învețe concepte ceva mai abstracte decât exemplele concrete. Thales a măsurat înălțimea piramidelor cu ajutorul umbrelor. Poți să faci și tu o astfel de exemplificare, cu ajutorul copacilor sau a clădirilor, folosindu-te de umbre.

Ce mai poți face este să demonstrezi vizual proporționalitatea segmentelor, folosindu-te de cretă și asfalt. Pentru elevi va fi mai interesant să vadă asta, decât să le exemplifici în modul clasic.

jocul și experimentele

Copiii pot învăța această teoremă mult mai ușor dacă o să le prezinți totul ca pe un joc. Îi poți ruga să măsoare diverse obiecte cu ajutorul umbrelor și a unei rigle, dar și să facă puzzle-uri cu triunghiuri din hartie, pentru a observa similitudinea.

folosește-te de tehnologiile moderne

Acum, în multe dintre școli există tehnologii moderne, care pot ajuta la un predat interactiv și la o înțelegere mai bună. Pe Internet vei găsi o mulțime de metode prin care teorema lui Thales este exemplificată, iar acestea pot duce la o înțelegere mult mai bună și mai ușoară.

În cazul în care ai nevoie de un exemplu practic prin care poți să ajuți elevii să înțeleagă mai ușor similitudinile, iată ce ai de făcut:

alege o perioadă a zilei în care vă puteți juca cu umbrele în exteriorul clădirii școlii;
identificați un stâlp care are o umbră bună și clară;
îndrumă elevii să măsoare propria înălțime, apoi înălțimea umbrei;
îndrumă elevii să măsoare apoi umbra obiectului.

După ce s-au făcut acești pași, explică-le că pot calcula foarte simplu înălțimea obiectului, folosind proporția teoremei lui Thales și anume:

Folosește-te de aceste informații și exemple și vei reuși să îți faci elevii să înțeleagă simplu și rapid această teoremă atât de importantă în matematică, dar și în viața de zi cu zi.

Teorema lui Thales – Formula și definiție