Peste tot în jurul nostru vedem triunghiuri, de la podurile caselor și semne de circulație, până la designul clădirilor și jucării. Această formă geometrică i-a fascinat și pe oamenii de știință de-a lungul timpului, care au studiat această formă pentru a-i afla toate secretele.
Acum, ceea ce dorim să facem în continuare este să îți vorbim despre triunghi, mai exact despre perimetrul său. Vom încerca să îți dezvăluim cele mai importante informații, pentru a înțelege totul cât mai bine.
Ce este perimetrul unui triunghi
Definiția perimetrului unui triunghi este una cât se poate de simplă. Așa cum învață elevii încă din clasa a IV-a și cum ne spune și GeoGebra, perimetrul unui triunghi reprezintă suma lungimilor tuturor laturilor. Este o explicație simplă și ușor de înțeles, acesta fiind și motivul pentru care se învață din clasele primare.
Perimetrul este o măsură liniară, care poate fi exprimat în centimetri, metri, kilometri și alte unități de măsură pentru lungime.
Și mai simplu de atât, perimetrul este practic toată marginea unui triunghi. Imaginează-ți că ai un triunghi pe care îl înfășori pe toate laturile cu o sfoară. Lungimea sforii care îl va cuprinde în totalitate reprezintă perimetrul.
De ce ne interesează perimetrul unui triunghi
În școală, adeseori, elevii se întreabă la ce le sunt necesare toate aceste noțiuni. Ei bine, peste ani, în practică, oamenii ajung să își dea seama de faptul că noțiunile de geometrie sunt extrem de utile. De exemplu, perimetrul unui triunghi are aplicabilitate într-o mulțime de domenii:
- construcții și amenajări
Dacă este necesar să construiești un gard în formă de triunghi, cum știi de câte materiale ai nevoie? Vei spune că aflînd cât de mare este gardul, nu? Corect. Și cum afli asta? Calculând lungimea totală pe care vrei să o obții, adică perimetrul.
- bricolaj
Când faci acasă tot felul de lucrări pentru renovări, amenajări etc., vei fi pus frecvent în situația de a lucru cu obiecte sau suprafețe în formă de triunghi. Pentru a obține rezultate cât mai precise și simetrice, vei avea nevoie să cunoști perimetrul unui triunghi.
- croitorie
Cei care lucrează în acest domeniu știu cât de important este să cunoască exact cât material trebuie să folosească la anumite piese vestimentare sau pe anumite zone. Cunoscând cum se calculează perimetrul unui triunghi, totul va fi mult mai simplu pentru a calcula materialul necesar.
- inginerie și arhitectură
În astfel de proiecte perimetrul este foarte important. Nu poți să cumperi materiale de construcție fără să știi exact de ce ai nevoie, de cantitatea necesară. Nimeni nu dorește să cumpere prea mult, nici prea puțin.
- mobilă și tâmplărie
Când lucrezi cu lemn, PAL sau alte materiale utilizate în realizarea de mobilă, din nou este important să știi să calculezi perimetrul, pentru a ști necesarul de material.
Acestea sunt aplicații practice în care este necesar să cunoaștem perimetrul. Dar, mai mult decât atât, cunoașterea acestor noțiuni ajută și la dezvoltarea elevilor. Ei își vor forma o gândire logică și matematică, vor conecta teoria cu practica și vor învăța să analizeze totul într-un mod cât mai eficient.
Cum se calculează perimetrul triunghiului
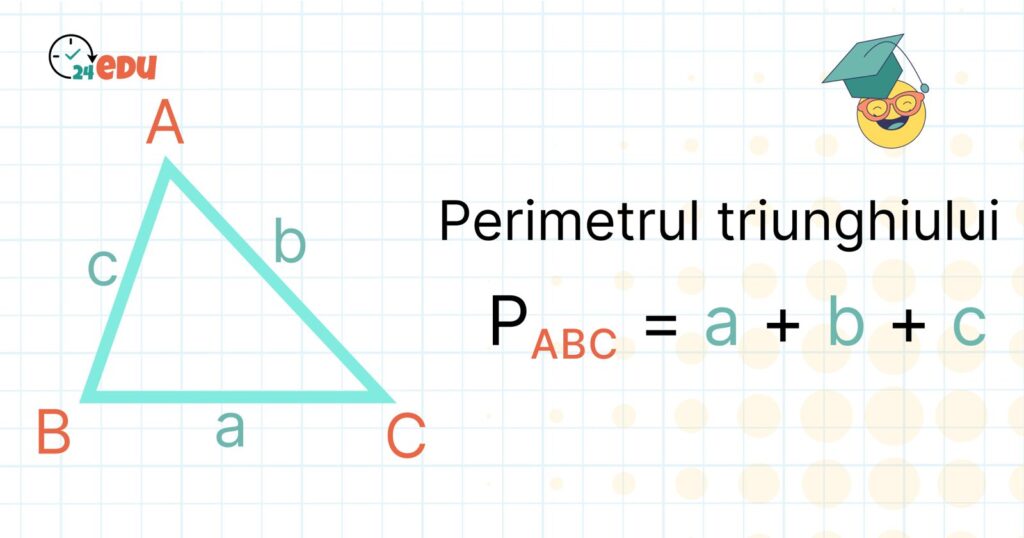
Perimetrul unui triunghi este foarte simplu de calculat și nu trebuie să faci altceva decât să aplici o formulă:
P = a + b + c
- a, b, c = lungimea laturilor
- P = perimetrul
Pentru a fi totul cât mai pe înțeles, se dă următorul exemplu:
Avem un triunghi ABC, cu laturile:
- AB = 5 cm
- BC = 7 cm
- CA = 6 cm
Pentru a-i calcula perimetrul aplicăm formula:
P = AB (a) + BC (b) + CA (c), mai exact P = 5 + 7 + 6 = 18.
Prin urmare, perimetrul acestui triunghi este egal cu 18 cm.
- Dacă este vorba de un triunghi echilateral (cu toate laturile egale), atunci se poate aplica și formula:
P = 3 x a, mai exact înmulțim cu 3 valoarea unei laturi
- Dacă este vorba de un triunghi isoscel (cu două laturi egale), atunci se poate aplica și formula
P = 2 x a + b, mai exact înmulțim cu 2 lungimea uneia din laturile egale și o adunăm pe cea de-a treia.
- Dacă toate laturile sunt diferite, adică dacă avem un triunghi scalen, aplicăm formula universală.
Exemple concrete de calcul
Pentru a te ajuta să înțelegi și mai bine perimetrul unui triunghi, îți vom da câteva exemple concrete de calcule:
Pentru triunghiul echilateral
Se dă triunghiul ABC, cu toate laturile egale. Lungimea unei laturi este de 10 cm.
Pentru a calcula perimetrul, aplicăm formula P = 3 x a, mai exact P = 3 x 10 = 30.
Așadar, perimetrul acestui triunghi este de 30 cm.
Pentru triunghiul isoscel
Se dă un triunghi ABC, cu două laturi egale. Lungimea fiecărei laturi egale este de 6 cm, iar cea de-a treia este de 4 cm.
Aplicând formula pentru triunghiul isoscel, mai exact P = 2 x a + b, obținem P = 2 x 6 + 4 = 16.
Prin urmare, perimetrul acestui triunghi este egal cu 16 cm.
Pentru triunghiul scalen
Se dă triunghiul ABC, cu toate laturile diferite. Lungimea acestora este de 5 cm, 7 cm, respectiv 8 cm.
În acest caz aplicăm formula universală pentru perimetrul triunghiului, mai exact P = a + b + C și obținem P = 5 + 7 + 8 = 20.
Perimetrul acestui triunghi va fi de 20 cm.
La ce trebuie să fii atent când calculezi
Pentru a obține rezultate corecte și pentru a nu te încurca în aceste calcule simple, este bine să ai în vedere o serie de aspecte:
- ține cont de unitățile de măsură folosite și asigură-te de faptul că toate sunt exprimate la fel. Dacă nu este așa, înainte de a face calculele, realizează și transformările necesare.
- dacă este vorba de o problemă de matematică, asigură-te de faptul că ai folosit corect toate datele problemei. Dacă e vorba de măsurători a unor suprafețe reale, verifică dacă le-ai măsurat corect.
Dacă vei face aceste două lucruri, totul va fi precis și te vei bucura de un calcul corect al perimetrului.
Perimetrul și geometria
În geometrie, perimetrul este esențial când vine vorba de înțelegerea proporțiilor și a diverselor dimensiuni pe care le au figurile geometrice. Dacă e să vorbim strict de triunghiuri, la acestea perimetrul este principala legătură dintre lungimea laturilor și forma geometrică per ansamblu.
Totodată, în geometrie, în momentul în care discutăm despre o figură închisă, putem vorbi și de perimetru, adică de lungimea laturilor sale. La triunghi, perimetrul se folosește atât pentru calcule simple, de bază, cât și pentru calcule mai complexe, în care se folosește și aria, unghiurile, construcții geometrice etc.
De exemplu, dacă într-un enunț al unei probleme ni se dă perimetrul total și două dintre laturi, putem afla cu ușurință dimensiunea celei de-a treia, formând o ecuație în care înlocuim valorile pe care le știm cu datele din problemă și aflăm necunoscuta.
În același timp, perimetrul este legat și de alte concepte foarte importante în geometrie:
- simetria – pentru a arăta echilibrul dintre laturile triunghiurile echilaterale și isoscele;
- congruența – pentru a arăta că două triunghiuri cu perimetrul egal și laturile egale sunt congruente;
- aria – valoare calculată frecvent împreună cu perimetrul.
Așadar, putem considera perimetrul un punct de plecare pentru înțelegerea mai profundă a conceptelor geometrice, a figurilor geometrice și a relațiilor dintre ele.
Curiozități despre triunghiuri
Triunghiurile sunt unele dintre cele mai interesante forme geometrice. Le întâlnim zilnic în jurul nostru și ascund o mulțime de informații interesante:
- triunghiul este considerat a fi cea mai stabilă formă geometrică, deoarece atunci când are laturile bine fixate, acestea nu se deformează la presiune. Astfel, el oferă o structură rigidă și sigură, fără a avea o diagonală de susținere cum este necesară adesea la formele pătrate sau dreptunghiulare.
- privite din unghiul corect, celebrele piramide egiptene sunt formate din patru triunghiuri isoscele. Acestea au permis realizarea unor construcții atât de stabile chiar și astăzi, după mii de ani.
- triunghiurile sunt forme foarte întâlnite în circulație. O mulțime de indicatoare rutiere sunt reprezentate de triunghi, mai ales cele de avertizare, exemplificate de un triunghi echilateral cu marginile roșii în care sunt desenate anumite semne care pot indica: curbe, îngustarea drumului, lucrări de întreținere, denivelări, intersecții, drum aglomerat, tunel, vânt lateral, urcare în pantă, coborâre periculoasă și multe altele.
- există un triunghi, triunghiul Penrose, care nu poate exista în realitate. Acesta este o iluzie optică întâlnită în artă sau jocuri de percepție, și are forma unui triunghi tridimensional.
- așa cum aflăm și de pe Matematica e Simplă, indiferent de modul în care este desenat un triunghi, unghiurile acestuia vor avea însumat 180 de grade. Aceasta regulă este baza multor demonstrații din matematică.
- triunghiul este prima figură geometrică cu interior, ce poate fi creată, deoarece are, așa cum îi spune și numele, trei laturi.
- stabilitatea unui triunghi se poate vedea și în triciclete, care, spre deosebire de biciclete, au mult mai multă stabilitate.
Verifică ce ai învățat despre perimetru
Credem că ai învățat destul de multe din acest text, pentru a fi capabil acum să îți testezi cunoștințele. Ești pregătit?
1. Perimetrul unui triunghi reprezintă:
a. suma unghiurilor sale
b. lungimea celei mai mari laturi
c. suma lungimilor tuturor laturilor
d. aria înmulțită cu înălțimea
2. Suma unghiurilor unui triunghi este:
a. 90 de grade
b. 180 de grade
c. 270 de grade
d. depinde de tipul triunghiului
3. Dacă avem un triunghi echilateral cu latura de 7 cm, perimetrul să va fi egal cu:
a. 14 cm
b. 21 cm
c. 28 cm
d. 7 cm
4. Un triunghi are laturile de 6 cm, 8 cm și 5 cm. Cât este perimetrul?
5. Un triunghi isoscel are două laturi de 9 cm și una de 7 cm. Cât este perimetrul?
6. Avem un triunghi cu perimetrul de 24 cm și două laturi de 8, respectiv 7 cm. Ce dimensiune are a treia latură?
7. Adevărat sau fals: Perimetrul unui triunghi se exprimă în centimetri pătrați.
8. Adevărat sau fals: Dacă avem un triunghi cu laturi de 3, 4 și 5 cm, perimetrul este 12.
Răspunsuri:
1. c – suma lungimilor tuturor laturilor
2. b – 180 de grade
3. b – 21 cm (P = 3 x 7 = 21 cm)
4. P = 6 + 8 + 5 =19 cm
5. P = 2 x 9 + 7 = 25 cm
6. 24 – (8+7) = 9 cm
7. Fals. Perimetrul se poate exprima în orice unitate de măsură pentru lungime (cm, m, km etc.).
8. Adevărat, deoarece P = 3 + 4 + 5 = 12 cm.
Jocuri și exerciții interactive
Învățarea prin joc a fost dintotdeauna mai interesantă și mai eficientă. Ce ai zice de câteva exerciții care te vor ajuta să vezi cât de distractivă poate fi de fapt matematica?
1. Identifică triunghiurile din cameră
Uită-te în jurul tău. Observă obiectele care te înconjoară. Analizează bine forma lor și descoperă-le pe cele care au forma unui triunghi.
Dacă este posibil, ia o riglă sau o ruletă și vezi ce dimensiune are fiecare latură, noteaz-o pe o bucată de hârtie, apoi calculează perimetrul respectivei suprafețe. Simplu și practic, nu-i așa?
2. Creează un triunghi
Ce ai zice să realizezi chiar tu un triunghi. Ai două variante: fie alegi întâmplător 3 obiecte care te pot ajuta să construiești un triunghi, indiferent de lungimea laturilor (bețișoare de frigărui, creioane, bețe de chibrit etc.), fie te gândești la dimensiunile pe care vrei să le aibă triunghiul tău și adaptezi apoi lungimea obiectelor din care vrei să-l construiești.
Dacă vrei să complici și mai mult acest exercițiu, poți construi atât triunghiuri echilaterale, cât și isoscele sau oarecare.
Acestea sunt două jocuri simple, care pot fi distractive pentru a-ți exersa cunoștințele în materie de matematică.
După cum ți-ai putut da seama din cele amintite mai sus, perimetrul unui triunghi nu este o simplă formulă matematică, ci este o noțiune pe care o poți întâlni zilnic în jurul tău, atât în construcții și design, cât și în semne de circulație sau croitorie.
Dacă ajungi să stăpânești aceste noțiuni, te vei dezvolta din punct de vedere intelectual și vei ști să îți ușurezi apoi viața când vei avea de calculat lungimea laturilor diverselor obiecte.
Da, poate nu o să te gândești că le vei calcula perimetrul, dar o sa pui de multe ori în practică aceste noțiuni fără să îți dai seama și fără să-ți amintești că le-ai învățat. De asta este matematica o știință atât de fascinantă.

Leave a Reply