Regula de 3 simplă este una dintre cele mai ușoare și mai utile metode de calcul folosite pentru a rezolva rapid probleme de proporționalitate. Se aplică atunci când trei valori sunt cunoscute, iar a patra trebuie aflată, cu condiția ca relația dintre ele să fie direct proporțională. Deși pare un concept simplu, regula de 3 simplă este prezentă în multe situații din viața de zi cu zi — de la calcule legate de cumpărături, rețete culinare, consum de combustibil, până la sarcini mai complexe din domeniul economic sau tehnic. Tocmai datorită versatilității și clarității sale, este una dintre primele noțiuni de matematică practică învățate în școală.
Cum funcționează regula de 3 simplă
Se aplică atunci când avem două mărimi care variază proporțional. Asta înseamnă că, dacă una dintre ele crește, și cealaltă va crește în același ritm, iar dacă scade, și cealaltă va scădea proporțional.
Sunt implicate patru elemente:
- Trei valori sunt cunoscute.
- A patra se calculează folosind o formulă de proporție.
Exemplu general:
Să presupunem că:
- 4 caiete costă 20 lei.
- Cât costă 6 caiete?
Se aplică proporția:
4 caiete → 20 lei
6 caiete → x lei
Se rezolvă astfel:
x = (6 × 20) / 4 = 30
Rezultat: 6 caiete costă 30 lei
Pașii de aplicare:
1. Identifică cele două mărimi legate între ele – de exemplu, cantitate și preț, timp și distanță etc.
2. Verifică dacă relația este direct proporțională – adică dacă dublarea primei mărimi duce la dublarea celei de-a doua.
3. Așază datele sub formă de proporție – două rapoarte egale.
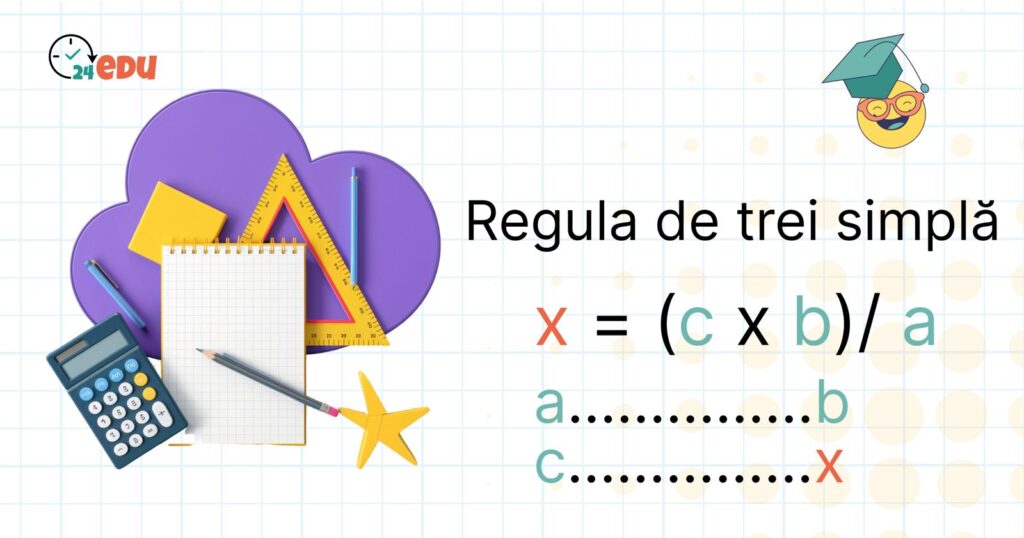
4. Aplică formula de calcul:
x = (a × c) / b
unde:
a și b sunt valorile cunoscute ale primei mărimi
c este valoarea cunoscută a celei de-a doua
x este necunoscuta de aflat
Când se folosește regula de 3 simplă
• În viața cotidiană – la cumpărături, când compari prețuri sau calculezi reduceri.
• În bucătărie – când adaptezi o rețetă la alt număr de porții.
• În călătorii – pentru a estima distanțe sau durate în funcție de viteză.
• În afaceri – pentru calcule rapide legate de profit, cheltuieli sau stocuri.
• În educație – ca bază pentru învățarea proporțiilor și a matematicii aplicate.
Unde se folosește în viața de zi cu zi – cu foarte multe detalii
Regula de 3 simplă este surprinzător de prezentă în viața de zi cu zi, chiar dacă nu o conștientizăm mereu. Ori de câte ori ne confruntăm cu probleme care implică proporții sau comparații directe între cantități, timp, prețuri sau resurse, folosim, de fapt, această metodă de calcul.
La cumpărături
Este poate cel mai frecvent loc unde aplicăm regula de 3 simplă:
- Exemplu: Dacă 2 kg de mere costă 14 lei, cât costă 3,5 kg?
Se aplică regula pentru a calcula rapid prețul pe baza prețului unitar sau pentru a compara oferte între produse. - Compararea reducerilor – Dacă 1 litru de ulei este 9 lei și o sticlă de 3 litri este 24 lei, care e mai convenabil?
• În bucătărie / gătit
Adaptarea rețetelor în funcție de numărul de porții presupune mereu o proporție:
- Exemplu: Dacă o rețetă pentru 4 persoane cere 300 g de orez, cât orez ai nevoie pentru 7 persoane?
Această ajustare se face simplu cu regula de 3, fără să schimbi gustul sau proporțiile ingredientelor.
• La calcule de combustibil și consum auto
Regula de 3 este foarte utilă când vrei să știi:
- Cât combustibil îți trebuie pentru un drum mai lung.
- Cât te va costa un drum în funcție de consumul mașinii.
- Exemplu: Dacă 100 km consumă 7 litri, câți litri îți trebuie pentru 250 km?
• În construcții sau bricolaj
Fie că zugrăvești o cameră, construiești un raft sau montezi gresie, calculele se bazează pe proporții:
- Exemplu: Dacă 5 litri de vopsea acoperă 35 m², câți litri sunt necesari pentru 56 m²?
• În economie personală
Folosim regula de 3 pentru:
- Calcularea salariului în funcție de ore lucrate.
- Estimarea economiilor sau cheltuielilor pentru un interval mai lung.
- Exemplu: Dacă economisești 300 lei pe lună, câți bani vei avea în 9 luni?
• În călătorii
Estimările de timp, distanță sau buget sunt des rezolvate cu regula de 3:
- Exemplu: Dacă trenul parcurge 120 km în 2 ore, cât durează să ajungă la 210 km?
- Sau: Dacă 1 euro e 5 lei, câți lei îți trebuie pentru 200 de euro?
• În activități casnice
Chiar și treburile gospodărești implică adesea calcule proporționale:
- Prepararea soluțiilor de curățare (raport între apă și detergent).
- Programarea mașinii de spălat în funcție de cantitatea de haine.
• În educație și teme pentru acasă
Copiii învață cu regula de 3:
- Proporții între numărul de exerciții și timpul de rezolvare.
- Compararea rezultatelor în funcție de efort (ex: dacă citești 30 de pagini în 2 ore, câte pagini citești în 5 ore?).
• În sport și fitness
Antrenamentele sau dietele presupun deseori calcule proporționale:
- Exemplu: Dacă alergi 5 km în 30 de minute, cât durează să alergi 8 km?
- Sau: Dacă un shake are 250 calorii la 300 ml, câte calorii sunt într-un pahar de 450 ml?
Regula de 3 simplă este, așadar, o unealtă matematică aplicabilă în zeci de situații cotidiene. Cunoașterea și folosirea ei corectă îți oferă eficiență, claritate și mai mult control asupra deciziilor de zi cu zi.
Formula de calcul pas cu pas
Pasul 1: Identifică mărimile proporționale
Trebuie să existe două mărimi între care există o relație direct proporțională.
De exemplu:
- Cantitate – Preț
- Distanță – Timp
- Număr de produse – Cost total
Important: regula de 3 simplă se aplică doar când mărimile cresc sau scad împreună.
Pasul 2: Așază datele cunoscute și necunoscuta sub formă de tabel sau proporție
Scrie-le clar, pe coloane:
| Mărimea 1 | Mărimea 2 |
| Valoare cunoscută A | Valoare cunoscută B |
| Valoare cunoscută C | x (necunoscuta) |
Exemplu:
- 4 produse costă 36 lei
- Cât costă 6 produse?
| Număr produse | Cost |
| 4 | 36 lei |
| 6 | x |
Pasul 3: Aplică formula matematică
Formula este:
x = (C × B) / A
Unde:
- A = prima valoare cunoscută din prima coloană (ex: 4 produse)
- B = valoare cunoscută din a doua coloană (ex: 36 lei)
- C = a doua valoare cunoscută din prima coloană (ex: 6 produse)
- x = necunoscuta
Pasul 4: Calculează
În exemplul nostru:
x = (6 × 36) / 4 = 216 / 4 = 54
Răspuns: 6 produse costă 54 lei
Pasul 5: Verifică logic răspunsul
Dacă 4 produse costă 36 lei, e normal ca 6 să coste mai mult.
Răspunsul de 54 lei are sens, deci calculul este corect.
Scurt rezumat:
• Scrii valorile în raport
• Aplici formula: x = (C × B) / A
• Calculezi și verifici dacă răspunsul e logic
Exemple practice explicate clar
1. Cumpărături – calcularea prețului pentru o cantitate diferită
Problema:
La magazin, 2 kilograme de portocale costă 15 lei. Cât vor costa 3,5 kilograme?
Rezolvare:
• Identificăm datele:
- 2 kg → 15 lei
- 3,5 kg → x lei (valoarea necunoscută)
• Aplicăm regula de 3 simplă:
x = (3,5 × 15) / 2 = 52,5 / 2 = 26,25 lei
• Interpretare:
3,5 kg de portocale costă 26,25 lei.
Este un exemplu foarte comun, folosit aproape instinctiv de mulți oameni atunci când vor să compare prețuri sau să cumpere cantități diferite față de cele afișate.
2. Gătit – adaptarea unei rețete
Problema:
O rețetă pentru 4 persoane conține 200 g de orez. Cât orez este necesar pentru 7 persoane?
Rezolvare:
• Datele sunt:
- 4 persoane → 200 g
- 7 persoane → x g
• Calculăm:
x = (7 × 200) / 4 = 1400 / 4 = 350 g
• Răspuns:
Ai nevoie de 350 g de orez pentru 7 persoane.
Astfel de calcule sunt foarte utile când vrei să adaptezi o rețetă pentru un alt număr de persoane, fără să pierzi echilibrul ingredientelor.
3. Transport – estimarea combustibilului necesar
Problema:
O mașină consumă 6 litri de combustibil pentru 100 km. Câți litri consumă pentru un drum de 180 km?
Rezolvare:
• Valorile cunoscute:
- 100 km → 6 litri
- 180 km → x litri
• Aplicăm regula:
x = (180 × 6) / 100 = 1080 / 100 = 10,8 litri
• Concluzie:
Pentru 180 km, mașina consumă 10,8 litri de combustibil.
Această aplicație este importantă pentru planificarea unei călătorii sau estimarea costurilor.
4. Timp de lucru – productivitate
Problema:
Dacă 3 muncitori finalizează o lucrare în 6 ore, câte ore le-ar lua la 2 muncitori?
Aici relația este invers proporțională, dar presupunem că folosim regula de 3 simplă în sens direct pentru o comparație parțială.
Soluție alternativă pentru direct proporțional:
Modificăm scenariul astfel:
Un muncitor finalizează o lucrare în 12 ore. Cât timp îi ia pentru 2 lucrări identice?
• Valorile sunt:
- 1 lucrare → 12 ore
- 2 lucrări → x ore
• Calcul:
x = (2 × 12) / 1 = 24 ore
• Interpretare:
Un muncitor va avea nevoie de 24 de ore pentru a face 2 lucrări identice.
În forma aceasta, problema respectă proporționalitatea directă și poate fi rezolvată cu regula de 3 simplă.
5. Salariu – venit calculat în funcție de ore lucrate
Problema:
Un angajat câștigă 2400 lei pentru 160 de ore lucrate într-o lună. Cât câștigă dacă lucrează doar 120 de ore?
• Valorile cunoscute:
- 160 ore → 2400 lei
- 120 ore → x lei
• Aplicăm regula:
x = (120 × 2400) / 160 = 288000 / 160 = 1800 lei
• Concluzie:
Pentru 120 de ore lucrate, angajatul va primi 1800 lei.
Această metodă este frecvent folosită pentru salarii part-time, proiecte la oră sau ore suplimentare.
6. Călătorii – estimarea timpului în funcție de viteză
Problema:
O bicicletă parcurge 12 km în 45 de minute. Cât timp va dura un traseu de 20 km?
• Datele sunt:
- 12 km → 45 min
- 20 km → x min
• Calcul:
x = (20 × 45) / 12 = 900 / 12 = 75 minute
• Răspuns:
Traseul de 20 km va dura 75 de minute.
Este un mod util de a estima timpul necesar pentru deplasare, fie că ești pe bicicletă, cu mașina sau pe jos.
7. Costuri la energie electrică
Problema:
Un aparat consumă 2 kWh pe zi și produce un cost lunar de 120 lei. Dacă este folosit doar 1,5 kWh pe zi, care va fi noul cost?
• Valorile proporționale sunt:
- 2 kWh → 120 lei
- 1,5 kWh → x lei
• Aplicăm formula:
x = (1,5 × 120) / 2 = 180 / 2 = 90 lei
• Concluzie:
Dacă reduci consumul zilnic la 1,5 kWh, factura va fi de aproximativ 90 lei.
Aceasta este o aplicație foarte practică în gestionarea consumului de energie în locuință.
Regula de 3 simplă este extrem de utilă într-o mulțime de contexte din viața reală. Fie că faci cumpărături, pregătești o masă, planifici o călătorie sau calculezi un salariu, această regulă te ajută să obții rapid rezultate corecte și logice.
De aceea, merită învățată bine, nu doar pentru școală, ci și pentru decizii mai bune în viața de zi cu zi.
Greșeli frecvente de evitat
• Confundarea proporționalității directe cu cea inversă
Aceasta este una dintre cele mai frecvente greșeli.
Exemplu greșit:
Dacă 4 muncitori termină o lucrare în 6 ore, câte ore le trebuie la 2 muncitori?
Unii aplică regula de 3 simplă ca și cum ar fi direct proporțional, dar în realitate este invers proporțional – mai puțini muncitori înseamnă mai mult timp.
Soluție corectă:
În astfel de cazuri, trebuie folosită regula de 3 inversă, nu cea simplă.
• Așezarea greșită a valorilor în proporție
Mulți înlocuiesc valorile în formula greșit, inversând ordinea coloanelor sau valorile între ele.
Exemplu greșit:
La întrebarea: „5 kg de cartofi costă 25 lei. Cât costă 8 kg?”, unii fac:
x = (5 × 8) / 25 – ceea ce este complet incorect.
Soluție corectă:
x = (8 × 25) / 5 = 40 lei
Sfaturi:
- Fă întotdeauna un mic tabel sau scrie logic valorile:
5 kg → 25 lei
8 kg → x lei
• Neglijarea unităților de măsură
Folosirea unităților neconcordante duce la rezultate complet greșite.
Exemplu greșit:
Dacă compari litri cu mililitri sau minute cu ore fără să le transformi înainte, rezultatul va fi greșit.
Soluție corectă:
Asigură-te că toate valorile sunt în aceeași unitate înainte de a aplica regula.
- 1 litru = 1000 ml
- 1 oră = 60 minute
• Aplicarea regulii în situații care nu sunt proporționale
Regula de 3 simplă se aplică doar în cazuri de proporționalitate directă.
Dacă relația dintre date este mai complexă, regula devine inutilă sau înșelătoare.
Exemplu greșit:
Temperatura vs. timp de fierbere – nu întotdeauna o creștere de 10 grade duce la o reducere proporțională a timpului.
Soluție:
Verifică dacă relația dintre mărimi este într-adevăr proporțională înainte de a aplica regula.
• Rotunjirea prea devreme sau incorect
Mulți fac greșeala de a rotunji prea devreme în timpul calculului și pierd acuratețea rezultatului final.
Soluție:
Fă toate calculele cu zecimale complete și rotunjește abia la final, dacă este necesar (ex: la bani, rotunjire la doi zecimale).
• Neglijarea logicii răspunsului
După calcul, unii nu se mai gândesc dacă răspunsul „are sens”.
Exemplu:
Dacă 4 produse costă 40 lei, iar cineva obține că 6 produse costă 20 lei – răspunsul este clar absurd.
Soluție:
Verifică logic: dacă „mai mult” ar trebui să însemne „mai scump” (în cazul proporționalității directe), atunci rezultatul trebuie să reflecte asta.
• Lipsa unei structuri clare în calcul
Oamenii sar direct la calcul fără să organizeze datele. Asta duce la confuzii.
Soluție:
• Scrie întâi relația completă (tabel sau linie cu săgeți)
• Verifică proporționalitatea
• Aplică formula
• Folosirea formulei greșite
Unii confundă regula de 3 simplă cu formule de medii, proporții procentuale sau alte calcule.
Exemplu:
Cineva ar putea calcula în loc de:
x = (a × c) / b, o formulă gen (a + c) / 2, care este complet irelevantă.
Chiar dacă azi tehnologia poate face aceste calcule instantaneu, logica regulii de 3 rămâne fundamentală, pentru că dezvoltă gândirea proporțională – importantă în viață, afaceri și decizii rapide.
Regula de 3 simplă nu a fost „inventată” de o singură persoană, ci a fost dezvoltată treptat de civilizații diferite – Egipt, Babilon, India, lumea arabă și Europa – ca răspuns la nevoile practice ale vieții: comerț, măsurare, schimb, organizare.
A fost transmisă de la o cultură la alta, rafinată și adaptată, iar astăzi este una dintre cele mai universale și durabile tehnici de calcul de bază.

Leave a Reply