Cercul circumscris este un concept fundamental în geometrie, care apare în mod natural atunci când lucrăm cu triunghiuri și alte poligoane. El are o importanță specială deoarece leagă noțiunea de cerc cu cea de figură poligonală, printr-o relație clară și elegantă.
• Definiția cercului circumscris
Conform Wikipedia, cercul circumscris al unui triunghi este cercul care trece prin toate cele trei vârfuri ale triunghiului.
Cu alte cuvinte, este un cerc care „încadrează” triunghiul, atingând fiecare colț al acestuia, dar fără a-l intersecta în alte puncte.
• Ce este centrul cercului circumscris
Centrul acestui cerc se numește circumcentru și are o proprietate specială:
Este situat la intersecția celor trei mediatoare ale laturilor triunghiului.
- Mediatoarea unei laturi este o dreaptă perpendiculară pe latură, care o împarte în două părți egale.
- Oricare două mediatoare se intersectează într-un punct comun, iar al treilea segment trece prin același punct – acesta este centrul cercului circumscris.
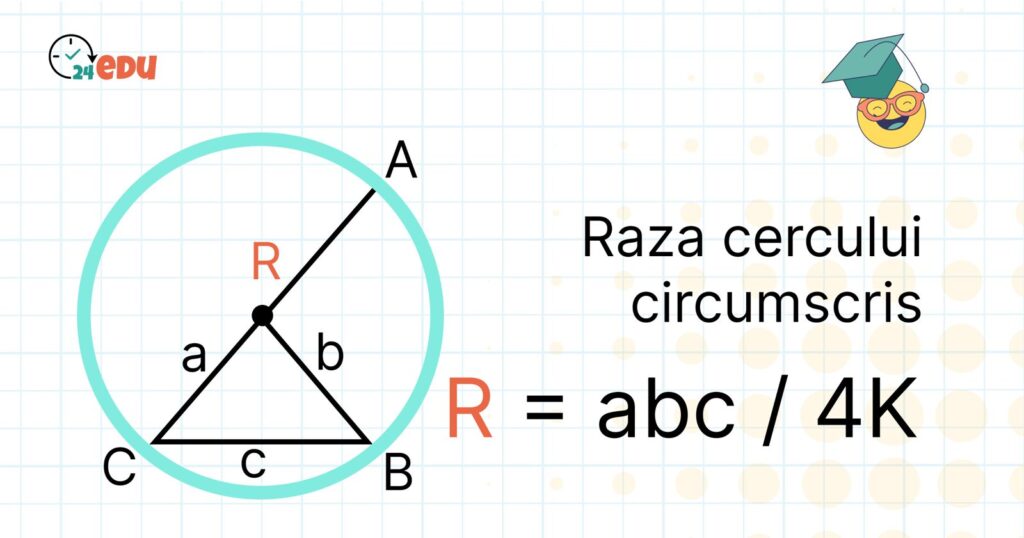
• Ce este raza cercului circumscris
Raza (notată cu R) este distanța de la centrul cercului (circumcentrul) până la oricare dintre vârfurile triunghiului.
Pentru că toate vârfurile se află pe cerc, distanțele sunt egale.
→ În orice triunghi:
RA = RB = RC = R
• Cum se construiește cercul circumscris (metodă geometrică)
1. Desenează triunghiul ABC
2. Construiește mediatoarea fiecărei laturi (AB, BC, AC)
3. Intersecția celor trei mediatoare = punctul O (centrul cercului)
4. Cu un compas, desenează un cerc cu centrul în O și raza până la A, B sau C
→ Cercul rezultat va trece prin toate cele trei puncte.
• Poziția centrului cercului în funcție de tipul triunghiului
| Tip triunghi | Poziția centrului cercului circumscris |
| Triunghi acutunghic | În interiorul triunghiului |
| Triunghi dreptunghic | La mijlocul ipotenuzei |
| Triunghi obtuzunghic | În exteriorul triunghiului |
• Exemplu simplu de înțeles
Imaginează-ți un triunghi ABC. Dacă desenezi un cerc care trece prin A, B și C, iar centrul acestui cerc este punctul O, atunci distanțele OA, OB și OC sunt egale – ele reprezintă raza R.
• Diferența față de cercul înscris
- Cercul circumscris trece prin vârfurile triunghiului
- Cercul înscris atinge laturile triunghiului, fiind situat în interiorul acestuia
→ Sunt cercuri diferite, cu formule și aplicații diferite
2. Importanța cercului circumscris în geometrie
Cercul circumscris nu este doar o figură frumoasă într-un desen geometric. El are un rol profund în înțelegerea structurii triunghiului și în rezolvarea multor probleme matematice și tehnice. În această secțiune, vei descoperi de ce cercul circumscris este important în geometrie, ce proprietăți are și în ce contexte devine util.
• Apare în toate triunghiurile
• Orice triunghi admite un cerc circumscris unic
Indiferent de forma triunghiului – acutunghic, obtuzunghic sau dreptunghic – există exact un singur cerc care trece prin cele trei vârfuri.
→ Acest fapt conferă stabilitate geometrică și face ca multe teoreme să fie aplicabile general.
• Este un element central în construcții geometrice
• Cercul circumscris este folosit pentru a construi sau verifica simetria
– Mediatoarele, perpendiculara pe laturi, echidistanța față de vârfuri – toate sunt legate de centrul cercului.
• Este o bază pentru construcții clasice cu riglă și compas
– Poți determina puncte notabile ale triunghiului cu ajutorul cercului circumscris.
• Permite aplicarea unor teoreme fundamentale
• Teorema sinusurilor
Aceasta este una dintre cele mai importante relații din trigonometrie:
a / sin A = b / sin B = c / sin C = 2R
Această relație leagă laturile triunghiului de unghiuri și de raza cercului circumscris.
→ Fără existența cercului circumscris, această formulă nu ar avea sens.
• Conectează geometria cu trigonometria
• Raza R apare în formule trigonometrice avansate
– În multe formule de arii, distanțe sau unghiuri, cercul circumscris este cheia.
– R apare în rezolvarea triunghiurilor folosind funcții sinus, cosinus etc.
• Apare frecvent în probleme și demonstrații
• Olimpiade și evaluări:
Problemele de geometrie din concursuri conțin adesea fraze precum „triunghiul are cerc circumscris de rază R” sau „punctul se află pe cercul circumscris”.
• Exerciții tipice:
– Calculul razei în funcție de laturi
– Determinarea unghiurilor folosind raza
– Aflarea poziției unui punct față de cercul triunghiului
• Permite demonstrații elegante
Folosind cercul circumscris, se pot demonstra proprietăți geometrice fără calcule complicate:
- Unghiul înscris într-un semicerc este drept
→ dovadă că într-un triunghi dreptunghic, cercul circumscris are centrul în mijlocul ipotenuzei - Punctele coliniare sau cociclice pot fi recunoscute cu ajutorul cercurilor circumscrise
→ aplicații în teorema lui Thales, teorema lui Miquel etc.
• Aplicații în geometria analitică și vectorială
Cercul circumscris poate fi exprimat și în coordonate (planul cartezian). Se poate calcula raza R folosind formule vectoriale sau pe baza distanțelor dintre puncte.
→ Acest lucru face ca cercul circumscris să fie important în probleme moderne de geometrie analitică, inclusiv în programare și grafică 2D.
• Este un reper pentru alte cercuri din triunghi
• Cercul înscris, cercurile exînscrise, cercul lui Euler, cercul celor nouă puncte – toate sunt analizate și construite în raport cu cercul circumscris.
→ El devine o referință centrală în studiul triunghiului.
3. Relația dintre triunghi și cercul circumscris
Fiecare triunghi are un cerc circumscris unic, dar poziția și proprietățile acestui cerc variază în funcție de tipul triunghiului. În continuare, vom analiza cum se comportă cercul circumscris în raport cu triunghiurile acutunghice, dreptunghice și obtuzunghice, și ce concluzii importante se pot trage din aceste diferențe.
• Triunghiul acutunghic
Definiție: toate cele trei unghiuri sunt mai mici de 90°.
Comportamentul cercului circumscris:
- Circumcentrul (centrul cercului) se află în interiorul triunghiului.
- Cercul „îmbrățișează” triunghiul uniform.
- Mediatoarele celor trei laturi se intersectează într-un punct situat în interior.
Exemplu:
Un triunghi cu unghiurile de 60°, 70° și 50° – cercul circumscris va fi poziționat simetric în jurul figurii.
• Triunghiul dreptunghic
Definiție: unul dintre unghiuri este de 90°.
Proprietate remarcabilă:
Circumcentrul este situat exact la mijlocul ipotenuzei.
→ Raza cercului circumscris este jumătate din ipotenuză.
De ce?
Pentru că unghiul drept este înscris într-un semicerc. Acest fapt duce direct la una dintre cele mai elegante teoreme:
Orice triunghi dreptunghic poate fi înscris într-un semicerc având ca diametru ipotenuza.
Exemplu:
Pentru un triunghi dreptunghic cu ipotenuza de 10 cm → raza cercului circumscris = 5 cm
• Triunghiul obtuzunghic
Definiție: unul dintre unghiuri este mai mare de 90°.
Comportamentul cercului:
- Circumcentrul este în exteriorul triunghiului.
- Deși cercul trece prin cele trei vârfuri, el trebuie să se „extindă” pentru a cuprinde un colț „deschis” al triunghiului.
- Mediatoarele laturilor se intersectează într-un punct aflat în afara figurii.
Exemplu:
Un triunghi cu un unghi de 120° – cercul circumscris va fi mare, iar centrul va fi poziționat în afara conturului triunghiului.
• De ce este importantă această relație
• Determină metoda de construcție
– Pentru triunghiuri obtuze, compasul trebuie deschis mai larg și centrul căutat în afara figurii.
• Afectează formulele și calculul razei
– În triunghiul dreptunghic, R = ipotenuză / 2
– În celelalte cazuri, trebuie folosită formula generală:
R = (abc) / (4 × A)
• Este importantă în rezolvarea problemelor geometrice
– Poziția centrului și lungimea razei influențează poziționarea altor puncte notabile (ortocentru, baricentru etc.)
4. Ce este raza cercului circumscris (notată R)
Raza cercului circumscris este una dintre cele mai importante mărimi asociate unui triunghi. Ea face legătura dintre geometria plană, trigonometrie și proprietățile triunghiului. În această secțiune, aflăm exact ce este raza R, cum o recunoști, cum o calculezi și ce semnificații are în funcție de context.
• Definiția razei cercului circumscris
Raza cercului circumscris (R) este distanța dintre centrul cercului (circumcentrul) și oricare dintre vârfurile triunghiului.
Pentru că toate cele trei vârfuri ale triunghiului se află pe cercul circumscris, raza este aceeași pentru fiecare dintre ele:
→ OA = OB = OC = R
Unde O este centrul cercului, iar A, B și C sunt vârfurile triunghiului.
• Ce exprimă de fapt raza R
Raza cercului circumscris exprimă cât de “larg” este triunghiul – adică dimensiunea minimă a unui cerc care îl poate încadra.
Cu cât triunghiul este mai deschis (unghi obtuz, laturi mari), cu atât R va fi mai mare.
• Când este raza ușor de aflat
• În triunghiul dreptunghic:
→ R este jumătate din ipotenuză
→ Ex: dacă ipotenuza = 10 cm, atunci R = 5 cm
• În triunghiul echilateral:
→ R se poate calcula direct în funcție de latură (vezi secțiunea următoare)
• În ce formule apare raza R
Raza cercului circumscris este parte importantă din:
• Teorema sinusurilor:
a / sin A = b / sin B = c / sin C = 2R
• Formula generală pentru R:
R = (abc) / (4 × A)
unde a, b, c sunt laturile triunghiului, iar A este aria
• Formule pentru triunghiuri speciale:
– triunghi echilateral: R = l / √3
– triunghi dreptunghic: R = ipotenuză / 2
• Ce influențează valoarea lui R
• Forma triunghiului:
– unghiuri mai ascuțite → R mai mic
– unghiuri obtuze → R mai mare
• Lungimea laturilor:
– laturi mai lungi → crește raza
– triunghi mic și compact → raza mică
• Aria triunghiului:
→ apare în formula: R = (abc)/(4 × A)
• Reprezentare grafică și intuiție
Imaginează-ți un triunghi trasat într-un cerc.
Distanța de la centrul cercului până la fiecare colț este R.
Cercul pare că „îmbrățișează” triunghiul exact, fără a-l depăși sau a-l intersecta altundeva.
5. Formula generală pentru raza cercului circumscris (R)
Pentru a calcula raza cercului circumscris unui triunghi, există o formulă generală care poate fi aplicată indiferent de forma triunghiului (acutunghic, dreptunghic sau obtuzunghic). Este una dintre cele mai folosite formule în geometrie și trigonometrie:
• Formula generală pentru R:
R = (a · b · c) / (4 · A)
• Ce reprezintă fiecare simbol
- a, b, c – lungimile celor trei laturi ale triunghiului
- A – aria triunghiului (atenție: nu este un unghi, ci aria exprimată în unități pătrate)
- R – raza cercului circumscris
• Cum se calculează pas cu pas
1. Calculează laturile a, b și c – fie din problemă, fie din coordonate, desen etc.
2. Calculează aria A a triunghiului – poți folosi:
– formula lui Heron, dacă știi toate laturile
– A = (b × h) / 2, dacă ai o înălțime
– A = (1/2) × ab × sin C, dacă ai două laturi și un unghi între ele
3. Aplici formula R = (abc) / (4A)
4. Obții raza R, în aceeași unitate ca laturile (cm, m, etc.)
Observații importante
• Aria A trebuie să fie exactă – orice greșeală în calculul ariei afectează direct rezultatul pentru R
• Laturile trebuie să fie exprimate în aceeași unitate – nu amesteca cm cu m
• Formula funcționează pentru orice triunghi, nu doar pentru cele „frumoase” sau regulate
• Când NU este ideal să folosești această formulă
– Dacă ai un triunghi dreptunghic → mai simplu folosești R = ipotenuză / 2
– Dacă știi două laturi și un unghi între ele → poți folosi formula trigonometrica:
R = a / (2 × sin A) (vezi secțiunea următoare)
6. Alte formule pentru R în funcție de cazuri speciale
Deși formula generală R = (abc)/(4A) funcționează în orice triunghi, există formule mai rapide și mai simple pentru cazuri speciale. Aceste formule sunt extrem de utile când nu cunoști toate laturile sau când ai informații legate de unghiuri. În plus, oferă o perspectivă mai trigonometrică asupra geometriei triunghiului.
• Formula în funcție de un unghi și o latură opusă
Dacă știi o latură și unghiul opus, poți calcula raza cercului circumscris astfel:
R = a / (2 × sin A)
Unde:
– a este latura cunoscută
– A este unghiul opus laturii a
– sin A este sinusul unghiului A
• Formula pentru triunghi dreptunghic
Dacă triunghiul este dreptunghic, atunci:

Aceasta rezultă direct din faptul că unghiul drept este înscris într-un semicerc.
• Formula pentru triunghi echilateral
Toate laturile și unghiurile sunt egale, deci raza se poate calcula astfel:
R = l / √3
Unde l este lungimea unei laturi.
• Variante echivalente ale formulei trigonometrice
Există și alte forme echivalente:
R = a / (2 · sin A)
R = b / (2 · sin B)
R = c / (2 · sin C)
→ Alegi formula în funcție de latura și unghiul cunoscut.
• Avantaje ale acestor formule speciale
• Mai rapide – nu necesită calculul ariei
• Mai directe – utile când ai deja măsurători de unghiuri
• Evită pași intermediari – ideali în probleme de concurs sau teste grilă
7. Exemple numerice complete – pas cu pas
Această secțiune include calcule complete ale razei cercului circumscris (notată cu R) pentru mai multe tipuri de triunghiuri: cu laturi cunoscute, triunghi dreptunghic, triunghi echilateral și cazuri în care se cunosc unghiuri și laturi. Fiecare exemplu este explicat clar și gradual.
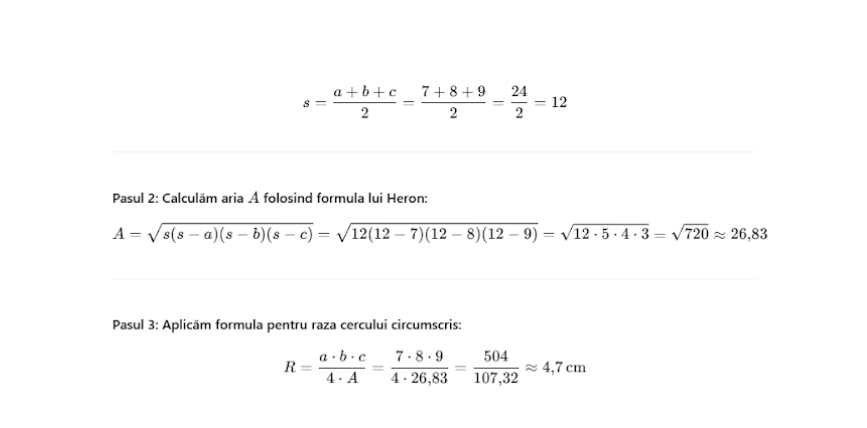
• Exemplul 1: triunghi cu laturile cunoscute
Date:
- a = 7 cm
- b = 8 cm
- c = 9 cm
• Exemplul 2: triunghi dreptunghic
Date:
– a = 5 cm
– b = 12 cm
– c = 13 cm (ipotenuză)
Observăm: 5² + 12² = 25 + 144 = 169 = 13² → deci e triunghi dreptunghic.
Folosim formula simplă pentru triunghi dreptunghic:
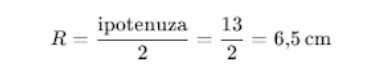
9. Greșeli frecvente de evitat
Chiar dacă formulele pentru raza cercului circumscris (R) sunt bine definite și relativ ușor de aplicat, mulți elevi sau chiar adulți fac greșeli atunci când le folosesc. Aceste erori pot duce la rezultate incorecte sau interpretări greșite în probleme. Iată care sunt cele mai comune greșeli și cum să le eviți:
• Confundarea cercului circumscris cu cel înscris
• Cercul circumscris trece prin vârfurile triunghiului
• Cercul înscris atinge laturile, din interiorul triunghiului
→ R ≠ r
Nu folosi formulele cercului înscris atunci când se cere raza cercului circumscris și invers.
• Alegerea formulei greșite
• Folosirea formulei R = c / 2 într-un triunghi care NU este dreptunghic
→ Această formulă este valabilă doar pentru triunghiuri dreptunghice, unde c este ipotenuza.
• Aplicarea R = a / (2 × sin A) fără unghiul A cunoscut
→ Dacă ai doar laturile, folosește mai întâi aria și formula generală.
• Calculul greșit al ariei (A)
• Erori în formula lui Heron:
– uitarea parantezelor
– rotunjirea prea devreme
– folosirea greșită a semiperimetrului
• Aria aproximativă = R greșit
→ Orice mică eroare în calculul ariei afectează direct valoarea razei.
• Folosirea laturilor în unități diferite
• Ex: a = 120 cm, b = 1,5 m, c = 2000 mm
→ Dacă nu convertești toate laturile în aceeași unitate, rezultatul va fi eronat.
Recomandare: convertește totul în metri sau centimetri înainte de calcul.
• Confuzie între funcția sinus și unghiul exprimat în grade
• Sin(30°) ≠ 30
→ Sin(30°) = 0,5 – trebuie folosit calculatorul în modul grade (nu radiani).
Greșeală comună:
– A calcula R = a / (2 × 30) în loc de R = a / (2 × sin 30°)
• Neatenție la rotunjiri
• Rotunjirea prea devreme sau prea agresivă
→ Evită să rotunjești prea devreme valorile intermediare (aria, sinusuri etc.)
Recomandare: păstrează 2–4 zecimale în pașii intermediari și rotunjește doar la final.
• Lipsa verificării logice
• Dacă ai un triunghi mic (ex: 3 cm laturi), R nu are cum să fie 20 cm
→ Fă un test de logică numerică asupra rezultatului. Dacă pare disproporționat, recalculează.
• Uitarea unității de măsură la răspuns
• R = 5 – dar 5 ce? cm? m?
→ Răspunsul trebuie însoțit de unitate de măsură.
• Omisiunea poziției centrului cercului în desen
• În triunghiuri obtuzunghice, centrul cercului circumscris este în afara triunghiului.
→ Dacă desenezi triunghiul și cercul, ia în calcul acest aspect.
Sfat practic:
Verifică întotdeauna dacă triunghiul este dreptunghic sau echilateral înainte de a decide ce formulă folosești pentru R.
Dacă nu e cazul special, folosește formula generală cu încredere.
10. Aplicații ale cercului circumscris în viața reală și știință
Deși pare un concept pur teoretic, cercul circumscris are multiple aplicații în domenii diverse precum arhitectura, ingineria, astronomia, geometria computațională sau chiar în artă. Acest cerc, care „îmbrățișează” un triunghi sau un poligon, oferă informații despre simetrie, echilibru, distanțe și proporții, utile în proiectare și analiză.
• Arhitectură și design structural
• Folosirea cercului circumscris în proiectarea clădirilor:
– Când se proiectează cupole, arcuri, bolți sau elemente circulare, triunghiurile și cercurile se combină în mod regulat.
– Prin înscrierea unui triunghi într-un cerc, arhitecții pot garanta simetrie și stabilitate.
• Structuri cu bază triunghiulară:
– Multe poduri, grinzi sau ferme metalice sunt construite pe baza de triunghiuri egale înscrise în cercuri, pentru a distribui greutatea în mod echilibrat.
• Inginerie civilă și mecanică
• Determinarea punctului de echilibru al unei structuri:
– Circumcentrul poate fi folosit ca punct de sprijin sau de fixare.
– În proiectarea pieselor rotative (roți, turbine, pale), centrul cercului circumscris este asociat cu axul de rotație ideal.
• Calculul distanțelor egale în structuri circulare:
– Prin poziționarea unor elemente (șuruburi, grinzi, elemente de fixare) în vârfurile unui triunghi echilateral înscris într-un cerc, se garantează distribuție egală a forței.
• Astronomie și fizică
• Orbitarea a trei corpuri cerești:
– Dacă trei obiecte (planete, sateliți) formează un triunghi în spațiu, raza cercului circumscris poate fi folosită pentru a calcula distanțe, traiectorii sau poziții orbitale.
• Geometria sferică:
– Pe o sferă, „triunghiurile” sferice pot fi proiectate într-un plan, iar cercul circumscris devine un element de analiză în calcule astronomice.
Geometrie computațională și grafică digitală
• Desenarea de forme echilibrate în software CAD și 3D:
– Motoarele grafice folosesc formulele cercului circumscris pentru a determina centri de simetrie, proporții, scalări.
• Algoritmi de detectare a coliniarității sau cociclicității:
– Programele de desen sau de analiză geometrică pot verifica dacă mai multe puncte sunt pe același cerc prin calculul razei și al centrului cercului circumscris.
• Artă și proporții clasice
• Arta geometrică:
– În construcțiile bazate pe triunghiuri regulate, cercul circumscris ajută la crearea de forme vizual echilibrate.
– Mandalele, vitraliile și mozaicurile conțin frecvent triunghiuri și cercuri interdependente.
• Proporțiile divine (ex: triunghi echilateral înscris în cerc):
– Raza devine o măsură simbolică de unitate și echilibru în artă sacră sau arhitectură religioasă.
• Matematică avansată și educație
• Probleme de olimpiadă și evaluare națională:
– Cercul circumscris este un element comun în probleme de dificultate medie și mare, în special în demonstrații geometrice.
• Relații între puncte notabile (ex: cercul celor nouă puncte, cercul lui Euler):
– Toate au legătură cu raza cercului circumscris și cu circumcentrul.
• Cartografie și geolocalizare
• Localizarea unui punct în funcție de 3 poziții cunoscute:
– În triangulație GPS, dacă ai trei puncte și vrei să determini o poziție exactă, centrul cercului circumscris oferă o soluție geometrică eficientă.
11. Exerciții de antrenament – cu rezolvări și verificări
🔹 Nivel ușor
1. Un triunghi dreptunghic are ipotenuza de 10 cm. Calculează raza cercului circumscris.
2. Într-un triunghi echilateral, latura are 6 cm. Află raza cercului circumscris.
3. Triunghiul ABC are unghiul A = 30° și latura opusă a = 8 cm. Calculează R.
🔹 Nivel mediu
4. Triunghiul are laturile a = 5 cm, b = 6 cm, c = 7 cm. Calculează raza cercului circumscris.
5. Un triunghi dreptunghic are catetele de 9 cm și 12 cm. Găsește raza cercului care îl încadrează.
6. Un triunghi cu laturile 13 cm, 14 cm, 15 cm trebuie înscris într-un cerc. Calculează R.
7. Se cunoaște că într-un triunghi, b = 10 cm și unghiul B = 60°. Află raza cercului circumscris.
🔹 Nivel avansat
8. Determină coordonatele centrului cercului circumscris unui triunghi cu vârfurile A(0, 0), B(6, 0), C(0, 8).
9. Arată că triunghiul cu laturi a = 6 cm, b = 8 cm, c = 10 cm este dreptunghic și calculează R.
10. Verifică dacă un triunghi cu R = 7 cm, latura a = 10 cm și unghiul A = 45° respectă formula R = a / (2 × sin A).
11. Pentru un triunghi cu s = 9 și A = √(9 × 4 × 3 × 2), calculează R dacă laturile sunt 5 cm, 6 cm și 7 cm.
Rezolvări și verificări
1. R = 10 / 2 = 5 cm
2. R = 6 / √3 ≈ 3,46 cm
3. R = 8 / (2 × sin 30°) = 8 / 1 = 8 cm
4.
- s = (5 + 6 + 7)/2 = 9
- A = √(9 × 4 × 3 × 2) = √216 ≈ 14,7
- R = (5×6×7)/(4×14,7) ≈ 210 / 58,8 ≈ 3,57 cm
5.
- ipotenuza = √(9² + 12²) = √(81 + 144) = √225 = 15
- R = 15 / 2 = 7,5 cm
6.
- s = (13 + 14 + 15)/2 = 21
- A = √(21×8×7×6) = √7056 ≈ 84
- R = (13×14×15)/(4×84) = 2730 / 336 ≈ 8,13 cm
7.
- sin 60° ≈ 0,866
- R = 10 / (2×0,866) ≈ 10 / 1,732 ≈ 5,77 cm
8.
- A(0,0), B(6,0), C(0,8)
- ipotenuză BC = √(6² + 8²) = √100 = 10
- centru = mijlocul ipotenuzei = (3, 4)
9.
- 6² + 8² = 36 + 64 = 100 = 10² → triunghi dreptunghic
- R = 10 / 2 = 5 cm
10.
- sin 45° = √2 / 2 ≈ 0,707
- R = 10 / (2×0,707) = 10 / 1,414 ≈ 7,07 cm
- Se respectă: 7 ≈ 7,07 → diferență minoră → OK
11.
- A = √(216) ≈ 14,7
- R = (5×6×7)/(4×14,7) ≈ 210 / 58,8 ≈ 3,57 cm
Raza cercului circumscris este un concept geometric simplu, dar puternic.
Te ajută să înțelegi structura triunghiului, să aplici teoreme importante și să rezolvi probleme din viața reală. Odată înțeleasă, această noțiune devine un instrument eficient în matematică și în gândirea logică.

Leave a Reply