Piramida este o figură geometrică tridimensională formată dintr-o bază poligonală și fețe laterale triunghiulare care se întâlnesc într-un punct comun numit vârf. Această formă este întâlnită frecvent atât în matematică, cât și în arhitectură sau artă, datorită structurii sale simple, dar stabile. În funcție de forma bazei, piramidele pot fi triunghiulare, pătrate, hexagonale și așa mai departe. Ele prezintă proprietăți geometrice interesante legate de suprafață, volum și simetrie, fiind studiate încă din
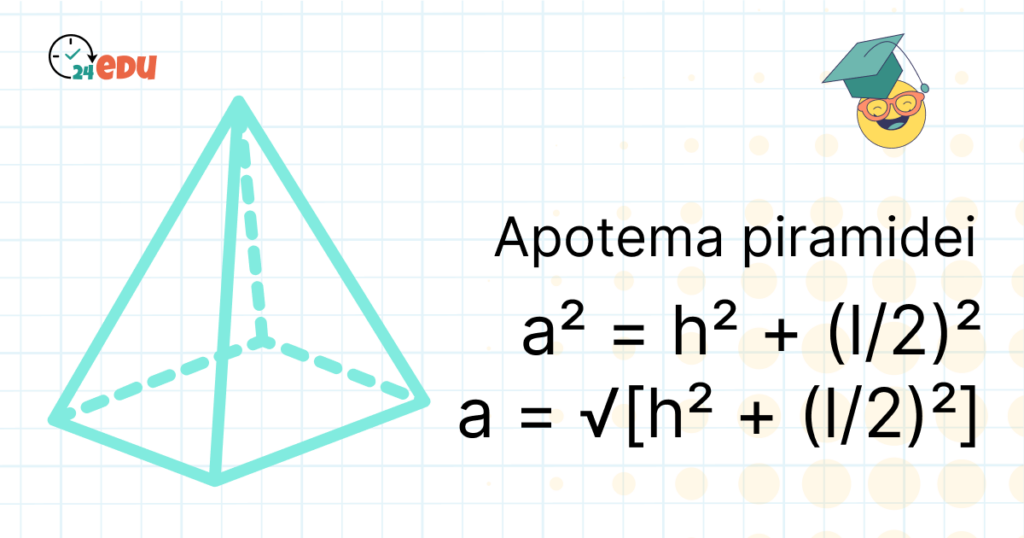
Ce este apotema piramidei?
Apotema piramidei este segmentul de dreaptă care unește vârful piramidei cu mijlocul unei laturi a bazei, fiind perpendicular pe acea latură. Se întâlnește doar în cazul piramidelor regulate, adică acelea care au baza un poligon regulat și fețele laterale triunghiuri isoscele congruente. Apotema este importantă în calcule geometrice, fiind folosită, de exemplu, pentru determinarea ariei laterale a piramidei.
Cum se calculează apotema piramidei?
Calculul apotemei piramidei se face folosind teorema lui Pitagora, într-un triunghi dreptunghic format din:
- vârful piramidei
- centrul bazei
- mijlocul unei laturi a bazei
Formula generală este:
a² = h² + (l/2)²
unde:
- a este apotema piramidei
- h este înălțimea piramidei (de la vârf perpendicular pe bază)
- l este lungimea unei laturi a bazei
Rezultă:
a = √[h² + (l/2)²]
Această formulă se aplică în cazul unei piramide regulate cu bază pătrată. Pentru alte tipuri de baze regulate (ex: triunghiulară, hexagonală), se adaptează în funcție de poziția centrului bazei față de latură.
Teoreme legate de apotema piramidei
Apotema unei piramide regulate este înălțimea unei fețe laterale triunghiulare. Aceasta poate fi determinată utilizând teorema lui Pitagora în triunghiul dreptunghic format de:
- vârful piramidei
- centrul bazei
- mijlocul unei laturi a bazei
În acest triunghi, conform Wikipedia, apotema piramidei reprezintă ipotenuza, iar celelalte două laturi sunt:
- înălțimea piramidei (segmentul de la vârful piramidei perpendicular pe bază)
- apotema bazei (distanța de la centrul bazei la mijlocul unei laturi a bazei)
Astfel, formula pentru calculul apotemei piramidei este:
a² = h² + ab²
unde:
- a = apotema piramidei
- h = înălțimea piramidei
- ab = apotema bazei
La ce se folosește apotema piramidei?
Apotema piramidei este folosită în principal în calculele geometrice legate de aria laterală și aria totală a unei piramide regulate.
- calculul ariei laterale
Aria laterală a unei piramide regulate este dată de formula:
A_l = (P_b × a) / 2,
unde:- P_b este perimetrul bazei
- a este apotema piramidei
Apotema reprezintă înălțimea fiecărei fețe laterale triunghiulare, așadar este importantă pentru a afla aria fiecărui triunghi lateral.
- calculul ariei totale
Pentru a afla aria totală a unei piramide, se adună aria bazei și aria laterală:
A_t = A_b + A_l,
deci apotema contribuie indirect la acest calcul. - aplicații practice
Se folosește în construcții, arhitectură, modelare 3D și desen tehnic, atunci când este nevoie să se calculeze suprafețe de acoperit sau materiale de folosit (ex: o piramidă decorativă, un acoperiș cu formă piramidală). - în probleme de geometrie
Apotema apare frecvent în probleme de tip examen sau olimpiadă, unde este cerut calculul unei dimensiuni necunoscute a piramidei folosind relații trigonometrice sau teorema lui Pitagora.
Alte linii importante in piramida
Într-o piramidă, pe lângă apotemă, mai există câteva linii importante, fiecare cu un rol geometric specific. Iată cele mai relevante:
- înălțimea piramidei
Este segmentul care unește vârful piramidei cu centrul bazei, perpendicular pe planul bazei. Este folosit frecvent în calcule de volum și în determinarea altor elemente geometrice. - muchiile laterale
Sunt segmentele care unesc vârful piramidei cu fiecare vârf al bazei. Într-o piramidă regulată, toate muchiile laterale sunt congruente. Pot forma fețele triunghiulare ale piramidei împreună cu laturile bazei. - apotema bazei
Este segmentul care unește centrul bazei cu mijlocul unei laturi ale bazei, perpendicular pe acea latură. Apare în multe formule, mai ales când se aplică teorema lui Pitagora în triunghiurile care includ apotema piramidei. - medianele fețelor laterale
În triunghiurile formate de fețele laterale, mediana este linia care unește vârful triunghiului (vârful piramidei) cu mijlocul bazei triunghiului (latura bazei piramidei). Este importantă în unele demonstrații geometrice sau construcții auxiliare. - diagonalele bazei
Dacă baza piramidei este un poligon cu mai mult de trei laturi (de exemplu, pătrat sau hexagon), diagonalele bazei pot fi relevante în probleme ce implică distanțe, simetrie sau secțiuni plan-paralele.
Cine a descoperit apotema piramidei?
Apotema piramidei, ca noțiune geometrică, nu a fost „descoperită” în sensul clasic, ci a fost dezvoltată treptat de matematicienii din Antichitate, în special de grecii antici care au pus bazele geometriei euclidiene.
Ce știm istoric:
- Egiptenii antici foloseau piramide în arhitectură (ex: Marea Piramidă din Giza), iar scrierile de pe papirusuri precum Papirusul Rhind (aprox. 1650 î.Hr.) conțin calcule care implică unghiuri și înălțimi, similare cu ce numim azi apotemă.
- Grecii, în special Euclid, au sistematizat noțiunile de geometrie în lucrarea sa Elementele. Acolo apar concepte legate de triunghiuri, înălțimi, simetrie și poligoane regulate – toate elemente importante pentru definirea apotemei.
- Apotema ca termen a fost introdus mai târziu, derivând din greaca veche „apotithenai” (a așeza deoparte). A fost folosită inițial în legătură cu poligoanele regulate, iar apoi extinsă și la piramide.
Așadar, nu putem atribui apotema unui singur „descoperitor”, ci mai degrabă unei evoluții lente a geometriei, începând cu egiptenii și formalizată de grecii antici.
Cine a fost Euclid și ce studii a făcut legat de piramidă?
Euclid a fost un matematician grec din secolul al III-lea î.Hr., cunoscut drept „părintele geometriei”. A trăit și a predat la Alexandria, în Egipt, în timpul domniei lui Ptolemeu I. Lucrarea sa principală, Elementele (Stoicheia), este una dintre cele mai influente cărți din istoria matematicii, folosită ca material didactic timp de peste 2000 de ani.
Cine a fost Euclid
- origine: Grecia antică
- locul activității: Alexandria, în cadrul faimoasei biblioteci
- perioadă: aprox. 300 î.Hr.
- lucrare principală: Elementele – 13 volume care acoperă geometria plană, teoria numerelor, proporțiile și corpurile geometrice
Ce studii a făcut legat de piramidă
În Elementele, în special în volumul XI și XII, Euclid studiază geometria în spațiu, iar piramida apare ca un corp geometric regulat. El:
- definește piramida ca fiind formată dintr-un poligon (baza) și triunghiuri ce se întâlnesc într-un vârf
- descrie proprietăți legate de muchii, fețe și înălțime
- demonstrează teoreme despre proporționalitate și arii, inclusiv metode de comparare între volumele piramidelor și ale prismelor
- deduce volumul piramidei ca fiind a treia parte din volumul unui prism cu aceeași bază și înălțime
De exemplu, Euclid a demonstrat (în mod geometric, fără formule algebrice) că:
Volumul unei piramide = (1/3) × Aria bazei × Înălțime
Nu folosea termenul „apotemă”, dar analiza liniile importante ale piramidei și relațiile dintre ele.
De ce este important ca elevii să învețe despre piramidă?
Învățarea despre piramidă este importantă pentru elevi din mai multe motive, care țin atât de dezvoltarea gândirii logice, cât și de aplicabilitatea practică a geometriei:
- dezvoltarea gândirii spațiale
Studiind piramida, elevii învață să vizualizeze obiecte în spațiu, să înțeleagă relații între dimensiuni (lungime, înălțime, arie, volum) și să își formeze o reprezentare tridimensională clară. - legături între geometria plană și cea în spațiu
Piramida face legătura dintre noțiuni cunoscute din plan (triunghiuri, poligoane) și corpurile geometrice. Astfel, elevii înțeleg cum pot fi extinse conceptele în contexte mai complexe. - aplicabilitate practică
Forma piramidală apare în arhitectură, artă, inginerie, chiar și în natură. Cunoașterea proprietăților unei piramide ajută la înțelegerea unor structuri reale sau la rezolvarea de probleme tehnice. - consolidarea logicii matematice
Problemele cu piramide implică adesea utilizarea teoremei lui Pitagora, a formulelor de arie și volum, și cer raționamente riguroase – dezvoltând astfel gândirea critică și capacitatea de argumentare. - pregătire pentru examene
Piramida este un subiect frecvent întâlnit în evaluări naționale, teze sau olimpiade, fiind un element important în programa de gimnaziu și liceu.
Prin studierea piramidei, elevii nu doar învață formule, ci își dezvoltă o înțelegere profundă a geometriei ca instrument de analiză a lumii reale.
Cum înveți elevii mai ușor despre piramidă?
Pentru ca elevii să învețe mai ușor despre piramidă, este important să se combine explicațiile teoretice cu metode vizuale, practice și interactive:
- folosirea de modele 3D
Construirea piramidelor din hârtie, carton sau materiale reciclabile îi ajută pe elevi să vadă și să atingă elementele: vârful, baza, muchiile, fețele, apotema, înălțimea. Acest contact vizual și tactil consolidează înțelegerea. - desene pe tablă sau în caiet
Schițarea piramidei cu toate liniile importante (înălțime, apotemă, muchii) și marcarea lor ajută la fixarea vizuală a relațiilor dintre ele. - utilizarea aplicațiilor sau simulărilor interactive
Există platforme (ex: GeoGebra, Mozaik3D) unde elevii pot roti piramide, modifica dimensiuni și observa efectele în timp real. Aceasta stimulează curiozitatea și interactivitatea. - analogii din viața reală
Compară piramida cu obiecte reale: corturi, acoperișuri, piramidele egiptene, prisme de sticlă. Aceste exemple îi ajută să lege teoria de lumea concretă. - jocuri și concursuri
Creează probleme tip puzzle sau competiții pe echipe: cine construiește o piramidă stabilă din bețe și plastilină sau cine rezolvă primul o problemă de volum. - explicarea în pași simpli și logici
Împarte lecția în etape clare: definirea piramidei, elementele ei, tipuri, formule, aplicații. Fiecare parte trebuie însoțită de un exemplu concret. - recapitulări vizuale și scheme
O schemă de sinteză colorată, cu toate conceptele-cheie, îi ajută să memoreze mai ușor și să facă legături între noțiuni.
Exemplu de plan de lecție
Obiectiv general
Elevii vor înțelege și identifica elementele componente ale unei piramide, vor învăța formulele de calcul și vor aplica cunoștințele în exerciții.
Durată: 50 de minute
1. Captarea atenției (5 min)
Activitate: Arată o imagine cu piramida din Giza și întreabă:
Ce formă are? Câte fețe are? Unde am mai văzut forme asemănătoare?
Scop: realizarea unei conexiuni între geometrie și viața reală.
2. Predarea noilor cunoștințe (15 min)
Explică:
- Ce este o piramidă
- Elementele piramidei: bază, vârf, fețe laterale, muchii, înălțime, apotemă
- Tipuri de piramide (regulată, neregulată)
Folosește:
- desen pe tablă
- un model 3D (fizic sau digital)
- evidențierea liniilor importante
3. Aplicarea cunoștințelor (15 min)
Exerciții propuse:
- identificarea elementelor unei piramide date (pe un desen)
- calcularea apotemei, ariei laterale sau a volumului (exerciții simple)
- completarea unei fișe cu desen și întrebări punctuale
4. Activitate practică (10 min)
Construiește cu clasa un model simplu de piramidă din carton/plastilină/bețe
- marchează pe model apotema și înălțimea
- discuție scurtă: La ce folosesc aceste linii în realitate?
5. Recapitulare și evaluare (5 min)
Joc tip quiz rapid:
- elevii răspund „adevărat/fals” sau aleg varianta corectă
- ex: Apotema este totuna cu înălțimea piramidei?
Temă pentru acasă:
Rezolvă 3 exerciții din manual + realizează o scurtă descriere a unei piramide reale (arhitecturală sau artistică) în 3-4 rânduri.
Apotema piramidei este un element important în studiul geometriei în spațiu, în special în cazul piramidelor regulate. Ea este definită ca segmentul care unește vârful piramidei cu mijlocul unei laturi a bazei, fiind perpendicular pe acea latură. Apare în triunghiurile isoscele care formează fețele laterale ale piramidei, unde joacă rolul de înălțime a triunghiului.
Importanța apotemei este dată de faptul că este folosită în formulele de calcul al ariei laterale și al ariei totale. De exemplu, aria laterală a unei piramide se calculează cu formula:
A_l = (P_b × a) / 2, unde a este apotema piramidei, iar P_b este perimetrul bazei. Apotema poate fi calculată folosind teorema lui Pitagora, într-un triunghi dreptunghic format de înălțimea piramidei, apotema bazei și apotema piramidei.
Această linie ajută la înțelegerea structurii interne a piramidei și la reprezentarea ei în desene tehnice. Cunoașterea apotemei contribuie la dezvoltarea gândirii geometrice și la aplicarea matematicii în probleme reale sau în proiecte de construcții.

Leave a Reply