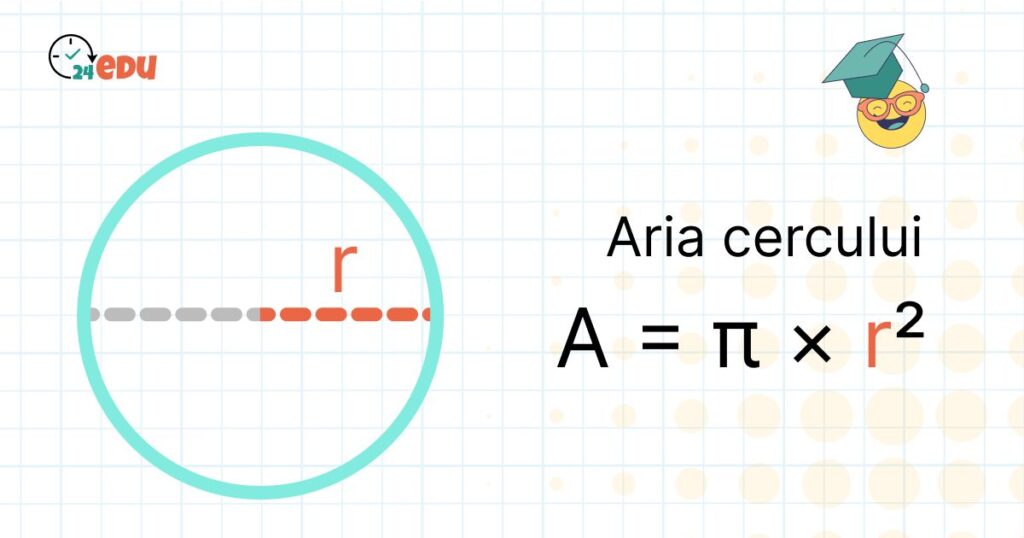
Aria cercului este un concept fundamental în matematică, care ne ajută să înțelegem cât spațiu ocupă un cerc pe o suprafață plană. Când vorbim despre arie, ne referim la suprafața cuprinsă în interiorul marginii cercului, adică între conturul rotund și centrul său. Este o idee ușor de imaginat dacă ne gândim la un obiect rotund, precum o farfurie sau o monedă – aria ne spune cât “loc” ocupă acel obiect pe masă. În viața de zi cu zi, cunoașterea ariei cercului ne poate fi utilă în diverse contexte, de la construcții și design, până la activități practice, cum ar fi decorarea unui tort sau calcularea suprafeței unui teren circular.
Cum a fost descoperită formula pentru aria cercului
Aria cercului este rezultatul a secole de observații, calcule și studii făcute de matematicieni din diverse culturi, iar istoria formulei se întinde din Antichitate până în epoca modernă.
În jurul anului 1800 î.Hr., babilonienii și egiptenii foloseau metode aproximative pentru a calcula aria cercului. De exemplu, în Papirusul Rhind, egiptenii estimau aria cercului considerând că este echivalentă cu aria unui pătrat al cărui latură este 8/9 din diametrul cercului, iar metoda dădea o valoare aproximativă pentru π (pi) de aproximativ 3,16.
Arhimede din Siracusa (287–212 î.Hr.) a fost primul care a oferit o demonstrație riguroasă și o metodă precisă de calcul a ariei cercului, folosind în acest sens o tehnică numită metoda exhaustivă, în care a înscris și circumscris poligoane regulate în jurul cercului, crescând treptat numărul de laturi. Pe baza acestora, a dedus că aria cercului este proporțională cu pătratul razei și a estimat valoarea lui π între 3,1408 și 3,1429.
În secolele V–X, matematicieni indieni precum Aryabhata și Brahmagupta au folosit valori mai precise pentru π și au lucrat cu formule legate de aria cercului. Ulterior, în lumea islamică, savanții precum Al-Khwarizmi și Alhazen au preluat și rafinat metodele grecilor, păstrând interesul pentru geometria cercului.
În secolul XVII, odată cu dezvoltarea calculului diferențial și integral de către Newton și Leibniz, formula pentru aria cercului a putut fi dedusă și prin metode analitice, integrând o funcție care descrie semicercul superior.
Această evoluție arată cum înțelegerea noastră despre cerc a crescut treptat, fiecare cultură contribuind cu idei care au dus la forma riguroasă a formulei cunoscută azi.
Care este definiția cercului?
Conform Wikipedia, cercul este o figură geometrică plană care reprezintă mulțimea tuturor punctelor aflate la o distanță constantă față de un punct fix numit centru. Această distanță se numește raza cercului. Cercul nu trebuie confundat cu discul, care este suprafața delimitată de cerc. Practic, cercul este doar conturul sau linia care închide spațiul interior.
Pe lângă centru și rază, un cerc mai are și alte elemente importante:
- Diametrul – segmentul care trece prin centru și unește două puncte de pe cerc; este egal cu de două ori raza.
- Coarda – un segment care unește două puncte de pe cerc, fără a trece neapărat prin centru.
- Arcul – o porțiune de cerc cuprinsă între două puncte.
- Secantă – o dreaptă care intersectează cercul în două puncte.
- Tangenta – o dreaptă care atinge cercul într-un singur punct.
Cum se calculează aria cercului
Aria cercului se calculează pornind de la ideea că suprafața ocupată de un cerc este proporțională cu pătratul razei sale, iar formula este simplă și se bazează pe o constantă foarte cunoscută în matematică:
A = π × r²
unde:
A este aria cercului
r este raza cercului (distanța de la centru până la margine)
π (pi) este o constantă aproximativ egală cu 3,14159
Exemplu practic:
Dacă ai un cerc cu raza de 5 cm, atunci:
A = π × 5² = π × 25 ≈ 3,14 × 25 ≈ 78,5 cm²
Provocări în calcularea ariei cercului
Una dintre provocările comune este rotunjirea valorii lui π (pi). Deoarece π este un număr irațional, elevii și chiar profesioniștii trebuie să decidă cât de precisă trebuie să fie valoarea folosită: 3,14; 22/7; sau cu mai multe zecimale (3,14159…) pentru că influențează exactitatea rezultatului, mai ales în calcule din inginerie, arhitectură sau știință.
O altă dificultate apare în identificarea corectă a razei, mai ales atunci când se oferă diametrul sau o altă mărime legată indirect de cerc. Mulți confundă raza cu diametrul, ceea ce duce la erori de calcul (deoarece formula implică pătratul razei, nu al diametrului).
În contexte reale, cum ar fi forme incomplete sau cercuri parțiale (semicercuri, sectoare circulare sau segmente circulare), apare provocarea de a adapta formula standard. În aceste cazuri, trebuie folosită o fracțiune din aria cercului complet, în funcție de unghiul sau secțiunea dată.
De asemenea, în aplicații precum teledetecția, designul asistat de calculator sau analizele topografice, unitățile de măsură și scalările pot complica calculul. Un cerc exprimat în pixeli sau în unități nedefinite necesită conversii suplimentare pentru ca aria să aibă un sens practic.
Pe lângă aceste aspecte, MathWorld subliniază și complexitatea istorică a demonstrației riguroase a formulei, care implică metode avansate precum limitele sau integrarea.
Prin urmare, deși formula ariei cercului este simplă în teorie, aplicarea ei corectă presupune atenție, înțelegere profundă și uneori adaptare la contextul în care este folosită.
Cum se folosește aria cercului în arhitectură?
În arhitectură, aria cercului este folosită pentru a calcula spațiile ocupate de elemente cu formă circulară, precum coloanele, ferestrele rotunde sau cupolele. De exemplu, atunci când un arhitect proiectează o clădire cu o cupolă, va trebui să știe cât spațiu va ocupa aceasta pe planșeu, pentru a o integra corect în structură. La fel, dacă o clădire are coloane cilindrice care susțin o fațadă, cunoașterea ariei bazei fiecărei coloane ajută la estimarea materialelor necesare și la echilibrarea proporțiilor.
De asemenea, în spațiile interioare sau în amenajarea curților, se pot include elemente decorative circulare – podele în formă de rozetă, fântâni sau scări în spirală care pornesc dintr-un punct central. În toate aceste cazuri, arhitectul folosește formula ariei cercului pentru a înțelege exact cât spațiu va ocupa fiecare element și pentru a-l încadra armonios în ansamblu.
Cum se folosește aria cercului în geografie?
Aria cercului este folosită pentru a calcula suprafețe de teren sau zone cu formă circulară, fie în mod direct, fie ca aproximare. Un exemplu des întâlnit este atunci când se studiază impactul unor fenomene naturale, cum ar fi erupțiile vulcanice, căderile de cenușă sau undele de șoc ale unui cutremur, care se extind adesea în mod circular de la un epicentru, iar specialistul are nevoie de formula ariei cercului pentru a determina câtă suprafață este afectată.
De asemenea, în analiza urbană sau în planificarea spațială, se folosesc zone tampon (buffer zones) în jurul unui punct de interes, cum ar fi o stație de transport, o sursă de poluare sau un centru de servicii, care au adesea formă circulară și ajută la estimarea populației afectate sau deservite într-o anumită rază.
Tot cu ajutorul ariei cercului se poate calcula acoperirea unei antene sau raza de influență a unei facilități (cum ar fi un spital sau o școală), pentru a analiza cât de bine este acoperită o regiune din punct de vedere al infrastructurii. În teledetecție și cartografie, când se măsoară imagini satelitare sau se delimitează regiuni de studiu, forma circulară este adesea aleasă pentru simplitate, iar calculul ariei ajută la interpretarea datelor spațiale.
Cum se folosește aria cercului în inginerie?
Aria cercului este utilizată aici pentru proiectarea, analiza și optimizarea multor componente și structuri care au secțiuni circulare. Un exemplu comun este în calculul suprafeței unei secțiuni transversale a unei bare, țevi sau cabluri, elemente care au adesea formă cilindrică. Cunoscând aria, inginerii pot determina rezistența materialului la forțe, cum ar fi compresiunea sau întinderea, lucru important în construcții sau în proiectarea mașinilor.
Tototdată, aria cercului este folosită pentru a calcula debitul de fluide care trec prin conducte. Dacă se cunoaște raza conductei, se poate determina cât lichid sau gaz poate trece într-un interval de timp, ceea ce este crucial în ingineria chimică, civilă sau energetică.
În ingineria mecanică, componente precum roțile, discurile de frână sau rulmenții implică frecvent forme circulare. Calculul ariei ajută la estimarea masei, a distribuției presiunii sau a eficienței în funcționare. Chiar și în domeniul electric, în proiectarea conductorilor sau a senzorilor circulari, aria joacă un rol important în evaluarea performanței.
Cum se folosește aria cercului în design și arte vizuale
Aici aria cercului este folosită pentru a planifica, echilibra și organiza compoziții care implică forme rotunde. Designerii grafici, de produs sau de interior lucrează adesea cu elemente circulare – logo-uri, butoane, rame, obiecte decorative – iar cunoașterea ariei le permite să controleze proporțiile și spațiul ocupat de fiecare formă în ansamblu.
De exemplu, într-un afiș sau o interfață digitală, un cerc poate fi folosit ca fundal pentru un element central. Dacă designerul trebuie să alinieze mai multe cercuri sau să le încadreze într-un spațiu limitat, va folosi aria pentru a calcula suprafețele și a păstra un echilibru vizual.
În artele vizuale, pictorii sau ilustratorii pot folosi forme circulare pentru a crea armonie și focalizare în compoziție. Aria cercului este importantă și atunci când se lucrează cu materiale – cum ar fi hârtia, pânza sau lemnul – iar artistul trebuie să știe câtă suprafață va acoperi cu o anumită culoare, textură sau detaliu.
Chiar și în designul obiectelor fizice, precum bijuterii, ceasuri sau mobilier, formele circulare sunt comune, iar aria ajută la estimarea materialelor necesare și la optimizarea formei în raport cu funcționalitatea și estetica.
Cum se folosește aria cercului în industria alimentară?
În industria alimentară, aria cercului este folosită frecvent pentru a calcula dimensiuni, porții și cantități atunci când produsele sau ustensilele au forme circulare. Un exemplu foarte comun este în cazul pizzei sau al torturilor rotunde. Producătorii și cofetarii folosesc aria cercului pentru a determina suprafața totală, astfel încât să poată împărți corect produsul în porții egale sau să stabilească prețul în funcție de mărime.
De asemenea, când se folosesc tăvi, forme sau ustensile rotunde, este important să se cunoască suprafața de contact cu aluatul sau compoziția. Acest lucru ajută la estimarea timpului de coacere, distribuirea uniformă a ingredientelor sau dozarea corectă a glazurii, cremei ori sosurilor.
În procesul de ambalare, aria cercului este folosită pentru a calcula cât spațiu ocupă un produs rotund în ambalaj sau pe o tavă de prezentare, ceea ce contribuie la optimizarea transportului și depozitării. De asemenea, în restaurante sau în producția de masă, acest calcul este util pentru standardizarea porțiilor, mai ales când produsele trebuie să aibă aceeași dimensiune pentru toți clienții.
Cum se folosește aria cercului în astronomie?
Aria cercului este folosită pentru a înțelege și calcula suprafețele aparent circulare ale unor obiecte sau fenomene observabile pe cer. Atunci când astronomii analizează discul aparent al Soarelui sau al Lunii, folosesc aria cercului pentru a estima câtă lumină sau energie ajunge pe Pământ din partea vizibilă a acestor corpuri.
Aria este importantă și în calcularea suprafeței secțiunii transversale a unei planete sau a unei stele, atunci când acestea sunt observate dintr-un anumit unghi. Chiar dacă corpurile cerești sunt sferice, din perspectiva noastră, ele apar ca niște discuri, iar pentru măsurători sau simulări, astronomii folosesc formule legate de aria cercului.
De asemenea, aria cercului se folosește în calcularea razei de acoperire a telescoapelor. Când un telescop „privește” spre cer, câmpul său vizual este adesea circular, iar astronomii trebuie să știe ce suprafață a cerului este inclusă într-o singură observație.
În studiile despre radiația solară, se calculează câte watt pe metru pătrat sunt primiți pe o suprafață circulară expusă la soare, ceea ce implică direct formula ariei. Tot așa, la lansarea sondelor sau în navigația spațială, aria circulară a motoarelor sau a scuturilor termice este importantă pentru calcularea forțelor și distribuției căldurii.
De ce este important ca elevii să știe cum se calculează aria cercului
Această noțiune îi ajută să înțeleagă mai bine lumea din jur și să dezvolte gândirea logică și spațială. Cercurile apar frecvent în viața de zi cu zi – de la roți, farfurii și capace, până la ceasuri, mese sau terenuri de sport. Când elevii știu cum să calculeze aria, pot aprecia cât spațiu ocupă un obiect, cât material este necesar pentru a-l acoperi sau cât costă un produs în funcție de dimensiune.
În plus, învățarea acestei formule îi ajută să facă conexiuni între matematică și alte domenii precum geometria, fizica, artele sau tehnologia. Calculul ariei cercului dezvoltă capacitatea de rezolvare a problemelor și îi pregătește pentru situații concrete, precum proiecte de design, planificarea unor spații sau chiar meserii din inginerie, arhitectură ori gastronomie.
Mai mult, înțelegerea ariei cercului nu este doar despre a memora o formulă, ci despre a înțelege cum funcționează proporțiile, formele și măsurătorile – abilități de bază pentru gândirea critică și raționamentul matematic.
Cunoașterea ariei cercului le oferă elevilor un instrument util pentru a înțelege și aplica matematica în contexte reale. De la obiecte simple din jurul lor până la fenomene complexe din știință și tehnologie, această noțiune geometrică stă la baza multor calcule și decizii practice. Se poate spune și că învățarea ariei cercului contribuie la dezvoltarea gândirii logice și a unei perspective mai clare asupra spațiului, formelor și proporțiilor.

Leave a Reply