Aria paralelogramului – Formula de calcul

Geometria plană este o ramură fundamentală a matematicii care se ocupă cu studiul formelor și figurilor în două dimensiuni. Printre figurile plane studiate încă din clasele primare se numără triunghiurile, dreptunghiurile, pătratele, romburile și, bineînțeles, paralelogramele.

2. Ce este un paralelogram?

Un paralelogram este un patrulater (o figură geometrică cu patru laturi) care are două câte două laturi opuse paralele și egale. Așadar, un paralelogram este o figură plană, convexă, ale cărei laturi opuse sunt situate pe drepte paralele.

Exemple de paralelograme:

• Dreptunghiul
• Pătratul
• Rombul
• Paralelogramul propriu-zis (fără unghiuri drepte sau laturi egale)

Proprietăți esențiale:

• Laturile opuse sunt egale și paralele.
• Unghiurile opuse sunt congruente.
• Diagonalele se înjumătățesc (se intersectează în mijloc).
• Orice paralelogram are simetrie centrală.
• Suma unghiurilor alăturate este de 180°.

3. Elemente ale unui paralelogram

Pentru a înțelege cum se calculează aria, trebuie să cunoaștem următoarele elemente:

• Baza (b): oricare dintre laturile paralelogramului, aleasă pentru calcul.
• Înălțimea (h): segment perpendicular pe baza aleasă, dus din vârful opus.
• Lungimea laturilor (a și b): două laturi consecutive pot fi luate drept bază și înălțime.
• Diagonalele: segmentele care unesc colțurile opuse.

4. Formula de calcul a ariei paralelogramului

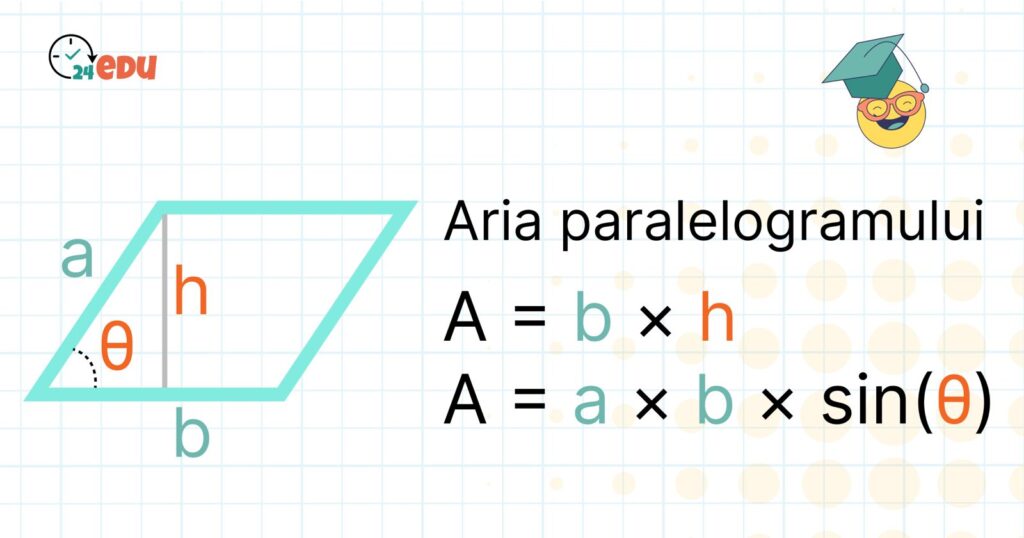
Aria unui paralelogram este spațiul cuprins în interiorul figurii și se calculează folosind formula:

A = b × h\textbf{A = b × h}A = b × h

Unde:

• A este aria, exprimată în unități pătrate (cm², m² etc.)
• b este baza
• h este înălțimea corespunzătoare bazei

Este important de știut că înălțimea trebuie să fie perpendiculară pe baza aleasă. Dacă se alege o altă latură ca bază, se folosește înălțimea corespunzătoare acesteia.

5. Justificarea formulei

Pentru a înțelege de ce A = b × h, putem folosi o abordare geometrică:

Imaginăm un paralelogram și “decupăm” un triunghi dintr-o parte pe care îl atașăm pe cealaltă parte. Obținem un dreptunghi. Astfel, aria paralelogramului este identică cu aria dreptunghiului, care se calculează tot prin înmulțirea bazei cu înălțimea.

Aceasta este o metodă intuitivă de a înțelege formula, folosită adesea în învățământul primar și gimnazial.

6. Exemple de calcul

Un paralelogram are baza de 12 cm și înălțimea de 5 cm. Care este aria?

Rezolvare:
Folosim formula:
A = b × h
A = 12 × 5 = 60 cm²

Răspuns: Aria paralelogramului este 60 cm².

Exemplul 2

O pajiște are formă de paralelogram cu baza de 30 m și înălțimea de 18 m. Care este suprafața pajiștii?

Rezolvare:
A = b × h
A = 30 × 18 = 540 m²

Răspuns: Suprafața pajiștii este 540 m².

Exemplul 3

Un paralelogram are aria de 150 cm² și baza de 10 cm. Care este înălțimea?

Rezolvare:
Folosim formula inversă:
h = A / b
h = 150 / 10 = 15 cm

Răspuns: Înălțimea paralelogramului este 15 cm.

7. Formula ariei folosind unghiul dintre laturi

Dacă nu avem înălțimea, dar cunoaștem două laturi consecutive și unghiul dintre ele, folosim formula:

Formula ariei paralelogramului folosind unghiul θ dintre laturi:

A = a × b × sin(θ)

unde:

• a și b sunt lungimile a două laturi consecutive ale paralelogramului,
• θ este unghiul dintre aceste laturi,
• sin(θ) este funcția sinus a unghiului θ.
  

8. Unități de măsură pentru arie

Unitățile în care se exprimă aria sunt întotdeauna unități pătrate, deoarece exprimă o suprafață bidimensională.

• milimetru pătrat (mm²)
• centimetru pătrat (cm²)
• metru pătrat (m²)
• kilometru pătrat (km²)

Este important ca toate măsurătorile folosite în formule să fie în aceleași unități.

9. Aplicații în viața reală

Calculul ariei unui paralelogram are numeroase aplicații:

• Construcții: calculul suprafeței unui acoperiș înclinat
• Agricultură: determinarea suprafeței unei parcele în formă de paralelogram
• Topografie: măsurarea terenurilor
• Design grafic: folosirea formelor geometrice în compoziții

10. Diferențiere față de alte figuri

Figură	Laturi egale	Unghiuri drepte	Arie
Paralelogram	Nu neapărat	Nu	A = b × h
Dreptunghi	Nu	Da	A = l × L
Pătrat	Da	Da	A = l²
Romb	Da	Nu	A = b × h sau (d₁ × d₂)/2

11. Probleme rezolvate

Problema 1:

Un paralelogram are baza de 14 cm și înălțimea de 9 cm. Calculați aria.

Rezolvare:
Folosim formula clasică:
A = b × h
A = 14 × 9 = 126 cm²

Răspuns: Aria paralelogramului este 126 cm².

Problema 2:

Un teren în formă de paralelogram are laturi de 24 m și 18 m, iar unghiul dintre ele este de 45°.

Rezolvare:
Folosim formula cu sinusul unghiului:
A = a × b × sin(θ)
A = 24 × 18 × sin(45°) ≈ 432 × 0,707 ≈ 305,42 m²

Răspuns: Aria terenului este aproximativ 305,42 m².

12. Exerciții propuse

1. Calculați aria unui paralelogram cu baza de 20 cm și înălțimea de 7 cm.
2. Dacă aria este 96 cm² și baza este 12 cm, care este înălțimea?
3. Un paralelogram are două laturi de 15 cm și 10 cm și un unghi de 30°. Care este aria?
4. Comparați aria unui pătrat și a unui paralelogram cu aceeași latură.
5. Un teren are forma unui paralelogram cu diagonale de 40 m și 60 m, iar unghiul dintre ele este de 90°. Care este aria aproximativă?

13. Greșeli frecvente de evitat

• Folosirea laturii ca înălțime dacă nu este perpendiculară.
• Calculul ariei cu formula greșită, de exemplu A = b × h / 2 (care este pentru triunghi).
• Neglijarea unghiului atunci când se folosește formula trigonometrică.
• Nerespectarea unităților de măsură – lungimea în metri, înălțimea în centimetri etc.

Aria paralelogramului este un concept geometric esențial care apare în numeroase situații din viața reală. Formula clasică A = b × h este simplă, dar cere atenție: trebuie folosită corect, iar înălțimea trebuie să fie perpendiculară pe baza aleasă.

Prin înțelegerea proprietăților și prin practică, calculul ariei unui paralelogram devine un instrument util și eficient. Elevii care înțeleg acest concept vor avea o bază solidă pentru studiul altor figuri geometrice și pentru aplicații în domenii precum arhitectura, ingineria, arta sau științele exacte.