Pătratul este un poligon regulat cu patru laturi egale și patru unghiuri drepte, reprezentând una dintre cele mai simple și totodată fundamentale forme din geometria plană. În matematică, studiul pătratului oferă un punct de plecare pentru înțelegerea conceptelor de simetrie, măsurători și relații între suprafețe. În viața cotidiană, pătratele apar în structura caramizilor, dale de gresie, plăci de lemn sau monocromie pe ecranele digitale, subliniind importanța calculului corect al ariei în proiecte practice.
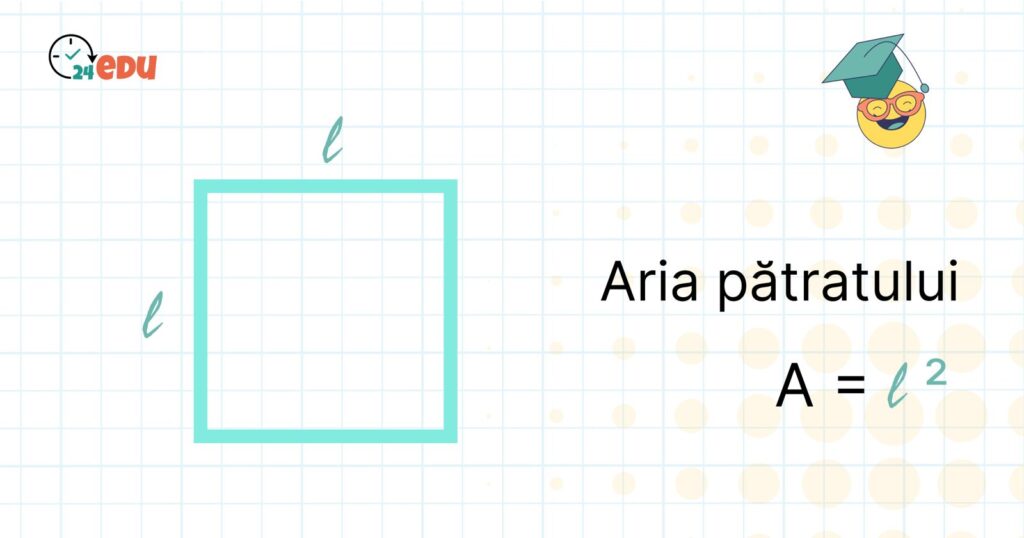
Calculul ariei pătratului se face cu o formulă extrem de simplă, dar cu un impact major:
- versatilitate: folosit pentru estimarea materialelor (hârtie, țiglă, parchet)
- precizie: latura pătratului definește direct suprafața, eliminând complicații inutile
- coerență: relația cu alte figuri plane (dreptunghi, romb, trapez) facilitează deduceri rapide
2. Definiția pătratului
Conform Wikipedia, pătratul este un poligon regulat cu patru laturi egale și patru unghiuri de 90°, fiind un caz particular de dreptunghi și de romb. Fiind atât de simplu, pătratul concentrează în sine toate proprietățile importante ale figurilor cu laturi și unghiuri egale.
Elemente componente ale pătratului
- laturile: toate cele patru segmente AB, BC, CD și DA au aceeași lungime, notată l.
- unghiurile: fiecare unghi interior măsoară exact 90°, făcând pătratul un poligon cu unghiuri drepte.
- diagonalele: segmentele AC și BD care unesc vârfurile opuse sunt egale ca lungime și se intersectează în unghi drept.
Proprietăți geometrice
- simetrie centrală: punctul de intersecție a diagonalelor este centrul de simetrie al pătratului.
- axe de simetrie: pătratul are patru axe de simetrie—două sunt mediatoarele laturilor, iar două sunt diagonalelor.
- diagonale perpendiculare: diagonalele se taie în unghi de 90° și își împart reciproc lungimea în două segmente egale.
Relații între elemente
Într-un pătrat cu latura de lungime l, lungimea diagonalei d se determină folosind teorema lui Pitagora:
d = l × √2
Aceasta rezultă din faptul că diagonala formează cu două laturi ale pătratului un triunghi dreptunghic isoscel.
Aria pătratului
Aria unui pătrat poate fi calculată în două moduri echivalente:
- Folosind latura:
A = l × l = l² - Folosind diagonala:
A = (1/2) × d²
Această a doua formulă rezultă din faptul că pătratul poate fi împărțit în două triunghiuri dreptunghice, fiecare cu baza și înălțimea egale cu lungimea diagonalei.
Reprezentare în plan cartezian
Un pătrat plasat convenabil în plan, cu un vârf în origine, are colțurile:
A(0, 0), B(l, 0), C(l, l), D(0, l)
Vectorii corespunzători laturilor sunt:
- AB = (l, 0)
- AD = (0, l)
Acești vectori sunt:
- Perpendiculare între ei
- Au lungimi egale, fiecare de lungime l
Aceasta confirmă că figura este un pătrat cu colțul A în origine și laturile paralele cu axele Ox și Oy.
Legătura cu alte poligoane
- pătratul este un dreptunghi cu laturile egale (L=lL = lL=l), deci proprietățile dreptunghiului se aplică.
- este un romb cu unghiuri drepte, deci toate proprietățile rombului (diagonale perpendiculare, bisectoare de unghi) sunt valabile.
- orice parallelogram cu unghiuri de 90° și laturi egale devine un pătrat.
3. Noțiunea de arie
Aria reprezintă mărimea suprafeței ocupate de o figură plană și este exprimată în unități pătrate. Pentru pătrat, aria indică câte „pătrățele” de latură 1 unitate se încadrează în interiorul său.
3.1. Definirea ariei
- Aria unui poligon plan este măsura regiunii pe care o acoperă în plan.
- În cazul pătratului, conturul său delimitează un spațiu uniform compus din pătrățele identice.
3.2. Unități de măsură
- milimetru pătrat (mm²) — pentru figuri foarte mici
- centimetru pătrat (cm²) — uz frecvent la școală și în design interior
- decimetru pătrat (dm²) — folosit în industrii de dimensiuni medii
- metru pătrat (m²) — standard în construcții, agricultură, arhitectură
- alte unități: kilometru pătrat (km²), hectar (ha = 10 000 m²)
3.3. Proprietăți ale ariei
- additivitate: aria reuniunii a două regiuni ne-împovărătoare este suma ariilor lor.
- invarianță la translație și rotație: mutarea sau rotirea figurii nu schimbă aria.
- scalare: dacă latura pătratului se mărește cu factorul kkk, aria crește cu k2k^2k2.
3.4. Importanța ariei pătratului
- Modelele de placare cu gresie sau mozaic în designul interior folosesc pătrate, iar calculul ariei directe simplifică estimările de material.
- În agricultură, parcelele dreptunghiulare echivalente cu pătrate idealizate se pot evalua rapid prin aria laturii.
- În grafică digitală, pixelii formează o grilă de pătrate, iar rezoluția ecranului este direct legată de numărul total de pixeli (aria în pixeli).
4. Derivarea formulei ariei pătratului
Formula ariei pătratului are o formă extrem de simplificată, datorită simetriei și regularității figurii. Dacă notăm cu lll lungimea laturii pătratului, atunci aria AAA se calculează prin:
A = l × l = l²
4.1. Argumentul „pătrățelelor”
Împarte latura pătratului în segmente de câte o unitate și trasează o grilă de linii paralele, orizontale și verticale. Astfel, pătratul va fi tăiat în l × l celule pătrate de latură 1.
Numărul total al acestor celule este l × l = l², ceea ce reprezintă aria pătratului, exprimată în unități pătrate.
4.2. Evocarea dreptunghiului echivalent
Pătratul este un caz particular de dreptunghi, în care toate laturile sunt egale (L = l). Aplicând formula pentru aria dreptunghiului (A = L × l), rezultă:
A = l × l = l²
Așadar, aria unui pătrat este dată de pătratul lungimii laturii sale.
4.3. Relația cu diagonala
Diagonala unui pătrat cu latura l are lungimea:
d = l × radical din 2
Dacă vrem să exprimăm aria pătratului în funcție de diagonală, folosim relația:
A = 1/2 × d²
Înlocuind d cu l × radical din 2, obținem:
A = 1/2 × (l × radical din 2)² = 1/2 × 2 × l² = l²
Aceasta confirmă că aria pătratului rămâne l², indiferent dacă este exprimată prin latură sau prin diagonală.
4.4. Generalizarea în plan cartezian
Calculul ariei pătratului prin integrare dublă
Plasăm pătratul în planul XY cu colțurile:
- A(0, 0)
- B(l, 0)
- C(l, l)
- D(0, l)
Pentru a calcula aria, folosim integrarea dublă pe domeniul pătratului [0,l]×[0,l][0, l] \times [0, l][0,l]×[0,l]:
A = ∫ de la 0 la l ∫ de la 0 la l (1) dy dx
Calcul pas cu pas:
- ∫ de la 0 la l (1) dy = l
- A = ∫ de la 0 la l (l) dx = l × l = l²
Rezultatul final este:
Aria A = l²
5. Exemple de calcul
Aplicarea formulei A = l² în practică
Pentru a vedea cum aplicăm formula A = l × l (aria unui pătrat), vom parcurge mai multe exemple cu laturi exprimate în diferite unități și contexte:
Exemplul 1: Pătrat cu latura în centimetri
Un pătrat are latura l = 7 cm.
Calcul:
A = l × l = 7 × 7 = 49 cm²
Rezultat: Aria pătratului este 49 cm².
Exemplul 2: Conversie în metri pătrați
Un pătrat are latura l = 150 cm.
Calcul:
A = 150 × 150 = 22.500 cm²
Conversie în metri pătrați (1 m² = 10.000 cm²):
A = 22.500 ÷ 10.000 = 2,25 m²
Rezultat: Aria este 2,25 m².
Exemplul 3: Pătrat digital (pixeli)
În grafică, un pătrat are latura de 320 pixeli.
Dacă 1 pixel ≈ 0,26 mm, atunci:
l = 320 × 0,26 = 83,2 mm
A = 83,2 × 83,2 ≈ 6.926,24 mm²
Conversie în centimetri pătrați (1 cm² = 100 mm²):
A ≈ 6.926,24 ÷ 100 = 69,26 cm²
Rezultat: Aria fizică a pătratului digital este aproximativ 69,26 cm².
Exemplul 4: Pătrat în amenajări interioare
O cameră pătrată are latura l = 3 m.
Calcul:
A = 3 × 3 = 9 m²
Rezultat: Avem nevoie de 9 m² de gresie (se recomandă un adaos de 5–10% pentru pierderi la tăiere).
Exemplul 5: Pătrat în agricultură
O parcelă de teren pătrată are latura l = 120 m.
Calcul:
A = 120 × 120 = 14.400 m²
Conversie în hectare (1 ha = 10.000 m²):
A = 14.400 ÷ 10.000 = 1,44 ha
Rezultat: Suprafața parcelei este 1,44 hectare.
6. Aplicații practice
- Design interior și amenajări
- Plăci de gresie și faianță: Cele mai comune dale au formă pătrată (ex. 30×30 cm). Cunoașterea ariei unui singur element ajută la calculul cantității necesare pentru acoperirea unui spațiu.
- Covorașe și mochetă: Pentru camere sau zone pătratice, aria directă din latură asigură achiziția exactă a materialului, minimizând risipa.
- Construcții și arhitectură
- Ferestre și uși: Ramele pătrate (la scară mică, cum ar fi ferestrele decorative) necesită calculul suprafeței sticlei pentru estimarea costurilor.
- Planșee modulare: Panourile de lemn sau beton prefabricate, adesea pătrate, se cuantifică prin aria laturii, optimizând stocurile și transportul.
- Industrie și ambalaje
- Etichete și pachete: Etichetele pătrate (ex. 5×5 cm) folosesc aria pentru imprimare și design grafic.
- Cutii și recipiente: Cutii pătrate la bază (înălțime variabilă) au suprafețe laterale și baze calculate pornind de la aria bazei pătrate.
- Tehnologie și grafică digitală
- Pixeli și rezoluție: Ecranele alcătuite din pixeli formați ca pătrate necesită calcularea numărului total de pixeli (latura în pixeli la pătrat) pentru definirea rezoluției.
- Pixel art și jocuri: Matricele pătratice simplifică generarea grafică și optimizarea fișierelor de imagine.
- Agricultură și silvicultură
- Zone experimentale: Parcelarea testelor pe suprafețe pătratice standard (ex. 10×10 m) permite comparații uniforme între diferite tratamente ale solului.
- Hectare echivalente: Convertirea rapidă a ariei pătratice în hectare sprijină planificarea culturilor.
- Activități cotidiene
- Tăvi și plăci de lemn: Piesele de mobilier cu suprafață pătratică (mese joase, tăvi) folosesc aria pentru finisaje și protecție (ulei, vopsea).
- Covorașe, perne și tapet: Modelele pătratice se calculează direct din latura pentru decupaje precise.
Prin stăpânirea ariei pătratului, elevul dobândește un pilon important pentru explorarea și calculul suprafețelor în geometrie, facilitând trecerea la figuri mai complexe și aplicații consacrate în diverse domenii.

Leave a Reply