Aria rombului este o noțiune fundamentală în geometrie, folosită pentru a determina suprafața ocupată de această figură plană. Rombul este un tip special de paralelogram, având toate laturile egale și proprietăți unice care îl diferențiază de alte patrulatere. Calculul ariei sale pornește de la înțelegerea acestor caracteristici, precum diagonalele sale care se intersectează perpendicular sau înălțimea care unește două laturi opuse. Cunoașterea modului în care se poate determina aria rombului este importantă în rezolvarea unor probleme geometrice, dar și în aplicații practice din arhitectură, design sau inginerie.
Ce este rombul?
Rombul este un patrulater convex care are toate cele patru laturi egale ca lungime. Este o figură geometrică plană și poate fi considerat un paralelogram cu laturi congruente. Pe lângă egalitatea laturilor, rombul are și alte trăsături distinctive: diagonalele sale se intersectează în unghi drept și se înjumătățesc reciproc, iar unghiurile opuse sunt egale.
Fiind o figură simetrică, rombul are o formă echilibrată și apare frecvent în context matematic, dar și în designul obiectelor sau în natură. Deși seamănă cu pătratul prin faptul că are laturile egale, rombul nu are neapărat toate unghiurile drepte.
Proprietățile rombului
Rombul are o serie de proprietăți geometrice care îl diferențiază de alte patrulatere și îl fac ușor de recunoscut:
Toate cele patru laturi sunt egale ca lungime
Conform Wikipedia, aceasta este caracteristica principală a rombului. Indiferent de forma unghiurilor, lungimea fiecărei laturi este identică.
Laturile opuse sunt paralele
La fel ca în cazul paralelogramelor, fiecare pereche de laturi opuse este paralelă, ceea ce înseamnă că nu se vor intersecta niciodată, oricât ar fi prelungite.
Unghiurile opuse sunt egale
Dacă un colț al rombului are un anumit grad, colțul opus va avea exact aceeași măsură. De asemenea, suma unghiurilor alăturate este de 180°.
Diagonalele se intersectează perpendicular
Acestea se taie în unghi drept (90°), formând patru triunghiuri dreptunghice în interiorul rombului.
Diagonalele se înjumătățesc reciproc
Punctul de intersecție al diagonalelor este mijlocul fiecărei diagonale, deci ele se împart în două segmente egale.
Diagonalele sunt și bisectoare ale unghiurilor
Fiecare diagonală împarte unghiurile din colțurile rombului în două unghiuri egale.
Are simetrie axială
Rombul are două axe de simetrie (cele două diagonale) și o simetrie de rotație de 180° în jurul centrului său.
Elementele definitorii ale rombului
Pentru a înțelege mai bine proprietățile și modul în care se poate calcula aria rombului, este important să cunoaștem elementele sale componente. Acestea sunt: laturile, unghiurile, diagonalele și înălțimea.
Laturile
Rombul este un patrulater ale cărui patru laturi sunt egale ca lungime. Această caracteristică îl face un caz special de paralelogram. Fie că un romb are unghiuri ascuțite sau obtuze, lungimea fiecărei laturi rămâne aceeași. Datorită acestei egalități, rombul se bucură de o simetrie laterală evidentă. În problemele geometrice, laturile rombului se notează de obicei cu litera a. Această latură este utilizată frecvent în formulele de calcul ale perimetrului sau ariei, în combinație cu alte elemente, precum înălțimea sau unghiurile.
Unghiurile
Chiar dacă toate laturile rombului sunt egale, unghiurile nu sunt neapărat drepte. În general, rombul are două unghiuri ascuțite și două unghiuri obtuze. Unghiurile opuse sunt întotdeauna egale, iar suma unghiurilor alăturate este de 180°, ca în orice patrulater. Un aspect important este că diagonalele rombului împart unghiurile în două unghiuri egale, fiind astfel și bisectoare. În unele exerciții, aria poate fi calculată cunoscând măsura unghiului dintre două laturi și lungimea laturii, folosind funcțiile trigonometrice.
Diagonalele
Rombul are două diagonale, care au un rol important în înțelegerea structurii sale. Acestea au următoarele proprietăți:
- se intersectează în unghi drept, formând patru triunghiuri dreptunghice în interiorul rombului;
- se înjumătățesc reciproc, punctul de intersecție fiind centrul simetriei rombului;
- sunt axe de simetrie ale rombului;
- sunt bisectoare ale unghiurilor, fiecare diagonală împărțind unghiurile din capetele opuse în două părți egale
Diagonalele sunt utile și în calculul ariei, existând o formulă specifică ce folosește doar lungimile lor.
Înălțimea
Înălțimea rombului este segmentul perpendicular dus de la un vârf la latura opusă (sau prelungirea acesteia). Reprezintă distanța dintre două laturi opuse și este perpendiculară pe una dintre laturi. Înălțimea este un element important în formula clasică de calcul a ariei: latură × înălțime. Deși mai puțin evidentă decât diagonalele, înălțimea reflectă „înălțimea reală” a rombului în raport cu baza aleasă și este importantă în problemele care implică spațiul ocupat de această figură.
Formula generală pentru aria rombului
Aria rombului poate fi calculată în mai multe moduri, în funcție de datele cunoscute. Formula generală clasică se bazează pe latură și înălțime:
A = latură × înălțime
Această formulă este similară cu cea a paralelogramului, deoarece rombul este un caz particular al acestuia. Înălțimea este segmentul perpendicular dus de la un vârf la latura opusă, iar latura este una dintre cele patru, toate fiind egale.
Pe lângă această formulă, există și alte variante care pot fi considerate tot formule generale, în funcție de informațiile disponibile:
Cu diagonalele:
Dacă sunt cunoscute lungimile celor două diagonale, aria se calculează astfel:
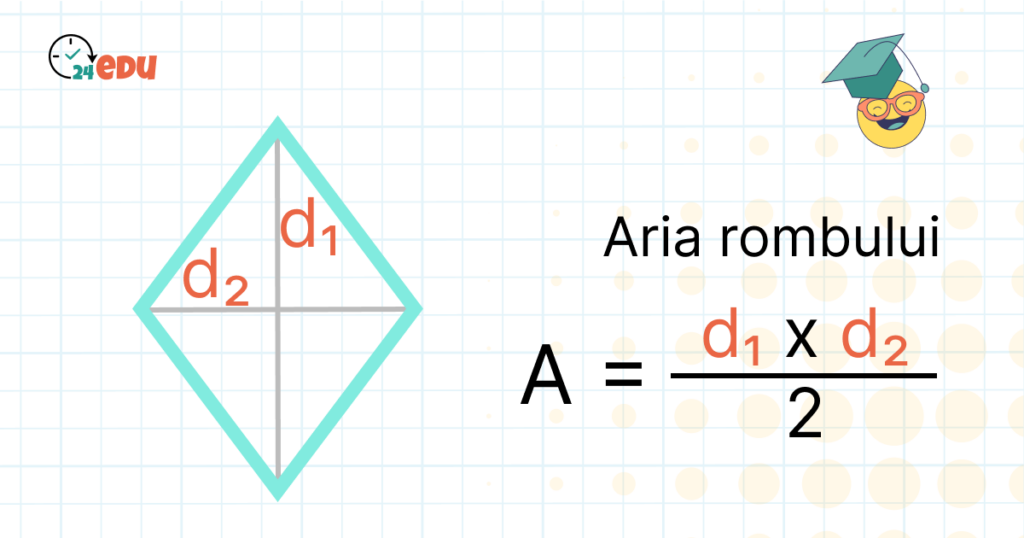
A = (diagonală mare × diagonală mică) / 2
Această formulă este foarte utilă, mai ales când înălțimea nu este dată, dar avem informații despre diagonale.
Cu latura și unghiul dintre laturi:
Când se cunoaște latura a și unghiul θ (theta) dintre două laturi alăturate, se poate folosi:
A = a² × sin(θ)
Aceasta implică o funcție trigonometrică și este folosită adesea în probleme mai avansate.
Indiferent de formula aleasă, toate conduc la același rezultat – măsura suprafeței ocupate de romb în plan.
Demonstrarea formulei pentru aria rombului
Pentru a înțelege mai bine de unde provin formulele pentru aria rombului, este util să vedem cum pot fi demonstrate cele mai folosite dintre ele.
Demonstrarea formulei A = latură × înălțime
Aceasta este cea mai intuitivă formulă și se bazează pe faptul că rombul este un tip de paralelogram. La fel ca la paralelogram, aria se calculează folosind baza și înălțimea corespunzătoare.
Să presupunem că rombul are latura a și înălțimea h, adică distanța perpendiculară dintre două laturi opuse. Dacă așezăm rombul pe o bază, iar înălțimea cade vertical pe această bază, putem observa că:
Figura poate fi „tăiată” și rearanjată într-un dreptunghi cu baza a și înălțimea h.
Aria unui dreptunghi este cunoscută: bază × înălțime.
Deci, și pentru romb, avem: A = a × h.
Aceasta este o demonstrație geometrică simplă, care arată că rombul „ascunde” un dreptunghi în structura sa.
Demonstrarea formulei A = (d₁ × d₂) / 2
Această formulă folosește diagonalele rombului, notate cu d₁ și d₂. Ele se intersectează în unghi drept și se înjumătățesc reciproc, formând patru triunghiuri dreptunghice egale.
Pașii demonstrației sunt următorii:Diagonalele se intersectează în unghi drept, deci rombul poate fi „împărțit” în două triunghiuri congruente prin fiecare diagonală. Mai exact, întreaga figură poate fi văzută ca fiind formată din două triunghiuri isoscele dreptunghice unite pe diagonală. Fiecare triunghi dreptunghic are catetele egale cu jumătățile celor două diagonale: d₁/2 și d₂/2.
Aria unui astfel de triunghi este: (1/2) × (d₁/2) × (d₂/2).
Avem patru astfel de triunghiuri în romb, deci aria totală devine:
4 × (1/2 × d₁/2 × d₂/2) = (d₁ × d₂) / 2
Această demonstrație se bazează pe simetria și structura rombului și arată cât de elegantă este geometria figurii.
Ambele demonstrații ne arată că, indiferent ce elemente avem date (laturi, înălțime, diagonale sau unghiuri), putem ajunge la calculul ariei printr-o logică clară și riguroasă.
Greșeli frecvente în aplicarea formulei
În rezolvarea problemelor de geometrie care implică aria rombului, apar adesea confuzii și greșeli, mai ales atunci când nu sunt înțelese corect elementele figurii sau se aplică automat formule fără a verifica condițiile problemei.:
Confuzia între înălțime și diagonală
Este una dintre cele mai frecvente greșeli. Mulți confundă înălțimea rombului cu diagonala mică sau mare, mai ales când problema este însoțită de un desen. Înălțimea este segmentul perpendicular pe o latură, nu diagonala care unește vârfurile opuse.
Aplicarea formulei cu diagonale fără să se cunoască ambele
Unii elevi folosesc formula A = (d₁ × d₂)/2 chiar dacă nu cunosc ambele diagonale, înlocuind-o pe una cu o altă dimensiune dată (cum ar fi latura). Este important ca ambele diagonale să fie cunoscute numeric sau exprimate corect.
Utilizarea greșită a funcției sinus
Când se aplică formula A = a² × sin(θ), o eroare des întâlnită este să se introducă unghiul în grade fără a verifica dacă instrumentul de calcul (calculatorul sau aplicația) este setat corect (în grade sau radiani). De asemenea, unii confundă sinusul unghiului intern cu sinusul unghiului exterior sau folosesc o valoare aproximativă eronată.
Aplicarea formulei pentru pătrat
Pentru că rombul are laturi egale, unii presupun greșit că aria se calculează ca la pătrat, adică A = latură², fără a ține cont de faptul că unghiurile nu sunt drepte. Această formulă este valabilă doar pentru pătrat, nu pentru orice romb.
Lipsa unităților de măsură sau combinarea lor greșită
O greșeală de neatenție este să se folosească unități diferite (de exemplu, latura în centimetri și înălțimea în metri) fără conversie, ceea ce duce la rezultate incorecte. Aria trebuie exprimată în unități pătrate, iar toate dimensiunile folosite trebuie să fie în aceeași unitate.
Identificarea greșită a liniilor
În unele probleme, desenul nu este proporțional sau poate induce în eroare. O greșeală frecventă este identificarea greșită a unei diagonale sau a unei înălțimi, ceea ce duce automat la aplicarea formulei greșite.
Neglijarea condițiilor problemei
Unii aplică automat o formulă fără să analizeze cu atenție datele sau să verifice dacă sunt suficiente informații. De exemplu, se încearcă calcularea ariei doar cu latura, fără înălțime sau unghi, ceea ce nu este posibil fără o relație suplimentară.
Evitarea acestor greșeli se poate face prin înțelegerea profundă a proprietăților rombului și printr-o analiză atentă a cerinței și datelor din problemă.
Aplicații ale rombului în viața reală și în geometrie
Rombul, deși este o figură geometrică simplă, are numeroase utilizări practice și teoretice. Proprietățile sale – precum laturile egale, diagonalele perpendiculare și simetria – îl fac util în contexte diverse, de la construcții și design până la rezolvarea problemelor matematice complexe.
Rombul este adesea folosit în designul pardoselilor, fațadelor și mozaicurilor datorită formei sale simetrice și estetice. Plăcile ceramice rombice pot crea modele vizuale dinamice, iluzie de profunzime sau mișcare. Arhitecții îl folosesc pentru a crea spații geometrice echilibrate și moderne.
În industria textilă, rombul apare frecvent în modele de țesături, broderii sau imprimeuri. Modelele în carouri (cum ar fi argyle) se bazează pe repetarea romburilor colorate, oferind un aspect clasic și elegant.
Unele indicatoare rutiere sau marcaje de avertizare folosesc forma de romb pentru a atrage atenția. În semnalizarea electrică sau în hărți, rombul poate marca intersecții, noduri sau puncte de interes.
În proiectarea structurilor metalice sau a rețelelor de susținere, forma de romb apare frecvent în grilaje și armături. Aceasta oferă un bun echilibru între stabilitate și flexibilitate.
În artă și decorațiuni, rombul este un element grafic versatil, folosit pentru a crea simetrie, contrast sau direcție. Se regăsește în vitralii, tapiserii sau obiecte decorative.
Aplicații în geometrie și matematică
Rombul este adesea folosit în exerciții matematice pentru a ilustra diverse metode de calcul al ariei – fie prin înălțime, fie prin diagonale sau funcții trigonometrice. Datorită proprietăților sale, este un exemplu excelent pentru aplicarea formulelor geometrice.
Forma rombului este utilă în studiul translațiilor, rotațiilor și simetriilor. Este folosit în demonstrații legate de simetrie axială și centrală sau pentru construcții geometrice.
În probleme avansate, rombul permite aplicarea funcțiilor trigonometrice, mai ales când se cunosc unghiurile sau se dorește calculul înălțimii pe baza laturii și a unui unghi.
În planul cartezian, rombul poate fi descris prin ecuații și vectori. Se folosește în exerciții de calcul al distanțelor, al unghiurilor dintre drepte sau în demonstrații de simetrie.
Prin urmare, rombul nu este doar o figură de manual, ci un model întâlnit frecvent în lumea reală și un instrument versatil în matematică. Forma sa simplă ascunde o geometrie bogată și elegantă, cu aplicații în numeroase domenii.

Leave a Reply