Aria trapezului – Formula de calcul

Trapezul este un poligon cu patru laturi, dintre care două sunt paralele și două sunt neparalele. Această formă geometrică apare frecvent atât în problemele de matematică, cât și în aplicații practice, de la designul arhitectural până la inginerie sau planificarea de grădini.

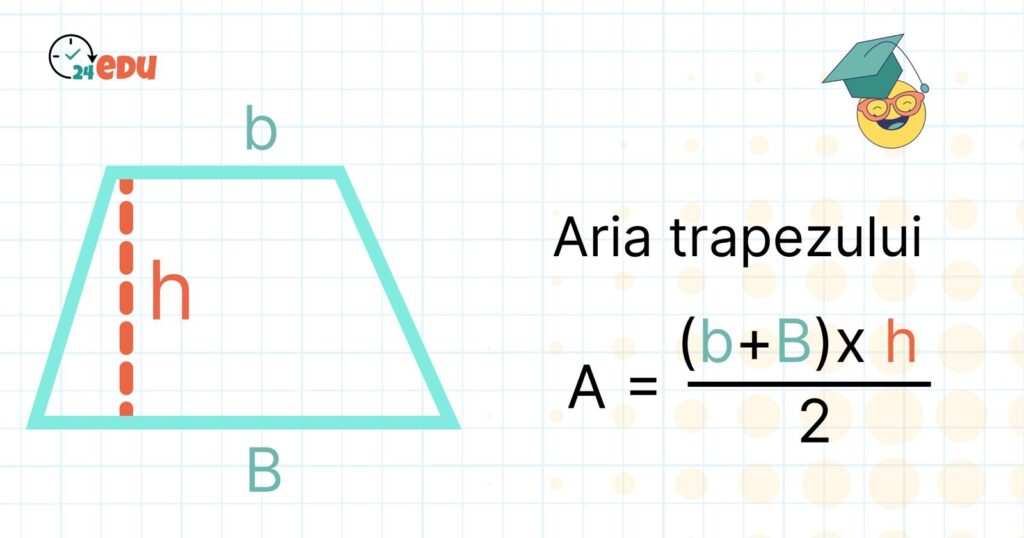
Conform CueMath, calculul ariei trapezului ne permite să determinăm suprafața unei figuri cu două baze de lungimi diferite, unite de laturi laterale care pot fi de înălțimi variabile. În viața reală, această măsură este utilă atunci când avem de acoperit, vopsit sau amenajat suprafețe trapezoidale, cum ar fi piese de mobilier, fațade înclinate sau parcele de teren cu margini neparalele.

2. Definiția trapezului

Trapezul este un poligon convex cu patru laturi, caracterizat prin existența a două laturi paralele numite baze. Restul două laturi, numite laturi laterale, pot avea lungimi diferite și formează marginile neparalele ale trapezului.

Elemente componente ale trapezului

Bază mare (B): latura paralelă superioară sau inferioară, mai lungă.
Bază mică (b): cealaltă latură paralelă, mai scurtă.
Laturi laterale (l₁, l₂): segmente care unesc capetele bazelor și nu sunt paralele între ele.
Înălțime (h): distanța perpendiculară dintre cele două baze.

Clasificarea trapezului

Trapez isoscel: laturile laterale au aceeași lungime; unghiurile de la baza mare și cea mică sunt perechi egale.
Trapez dreptunghic: o latură laterală este perpendiculară pe baze; are unghi de 90° la o singură extremitate a fiecărei baze.
Trapez oarecare: laturi laterale de lungimi diferite și unghiuri diferite; nu are niciuna dintre proprietățile trapezelor isoscel sau dreptunghic.

3. Metode de calcul

Pentru a determina aria unui trapez, putem recurge la două abordări principale:

1. Decompoziția în triunghiuri și paralelograme

Trasăm o înălțime dintr–un vârf al bazei mici până pe baza mare, obținând un triunghi dreptunghic și un trapez dreptunghic mai mic.
Continuând descompunerea, putem transforma întreaga figură într-un paralelogram sau două triunghiuri, al căror aria se calculează simplu prin formulele cunoscute:
- Aria triunghiului = (1/2) * baza * inaltime
- Aria paralelogramului = baza * inaltime

2. Formula generală
Fără să mai facem descompuneri, există o formulă directă pentru aria trapezului, bazată pe media bazelor și înmulțirea cu înălțimea:

A = ((B + b) * h) / 2

unde:

B = baza mare
b = baza mică
h = înălțimea

4. Formula ariei trapezului

Pentru a calcula rapid aria unui trapez, folosim formula:

A = ((B + b) * h) / 2

unde:

A este aria trapezului,
B este lungimea bazei mari,
b este lungimea bazei mici,
h este înălțimea trapezului (distanța perpendiculară dintre cele două baze).

Derivare intuitivă

Media bazelor
- Se calculează media aritmetică a lungimilor celor două baze: (B + b) / 2
Echivalență cu paralelogramul
- Gândiți-vă că ați „umple” trapezul cu un paralelogram care are baza egală cu media bazelor trapezului și aceeași înălțime. Aria paralelogramului este baza înmulțită cu înălțimea:
- ((B + b) / 2) × h
Aplicarea formulei
- Rezultatul este tocmai aria trapezului, fără a mai descompune figura.

Interpretarea termenilor

(B+b)(B + b)(B+b) reprezintă suma lungimilor bazelor, deci „totalul” pe care îl împărțim la 2 pentru a obține o bază echivalentă mediată
Multiplicarea cu hhh extinde acest segment echivalent pe toată înălțimea trapezului, obținându-se astfel suprafața completă.

5. Exemple de calcul

Pentru a vedea cum se aplică în practică formula

A = ((B + b) × h) / 2

vom parcurge câteva situații concrete:

Exemplul 1: trapez cu baze și înălțime cunoscute

Fie un trapez cu B = 12 cm, b = 8 cm și h = 5 cm.

Aria trapezului se calculează cu formula:
A = ((B + b) × h) / 2

Înlocuind valorile:
A = ((12 + 8) × 5) / 2
A = (20 × 5) / 2
A = 100 / 2
A = 50 cm²

Exemplul 2: transformarea într-un trapez izoscel

Dacă trapezul are B = 15 m, b = 9 m și h = 4 m, atunci:

A = ((15 + 9) × 4) / 2 = (24 × 4) / 2 = 96 / 2 = 48 m²

Exemplul 3: aplicație în grădinărit

O parcelă trapezoidală are bazele de B = 30 m și b = 20 m și o înălțime de h = 10 m. Câte metri pătrați de pământ trebuie pregătiți?

A = ((30 + 20) × 10) / 2 = (50 × 10) / 2 = 250 m²

Exemplul 4: suprafață de vopsit

Un perete cu formă trapezoidală are baza de sus b = 2 m, baza de jos B = 4 m și înălțimea h = 3 m. Câtă vopsea este necesară pentru a acoperi suprafața (fără calculul consumului pe metru pătrat)?

A = ((4 + 2) × 3) / 2 = (6 × 3) / 2 = 9 m²

Exemplul 5: conversie între unități

Dacă obținem un rezultat de A = 75 cm² dintr-un trapez cu B = 20 cm, b = 10 cm și h = 5 cm, iar suprafața trebuie exprimată în decimetri pătrați:

75 cm² = 0,75 dm²

6. Aplicații practice

Calculul ariei trapezului are numeroase utilizări în domenii variate, deoarece multe structuri și suprafețe din viața reală au formă trapezoidală.

Arhitectură și design interior

Trapezele apar în planurile de fațade înclinate, grinzi și stâlpi cu secțiune trapezoidală.
Designerii de amenajări interioare folosesc trapeze pentru elemente de pardoseală decorative, trepte de scară și balustrade.

Inginerie și construcții

Calculul ariei secțiunii transversale a unor canale trapezoidale de scurgere sau a barajelor cu profil trapezoidal.
Determinarea suprafeței laterale a elementelor prefabricate (panouri, grinzi) cu secțiune trapezoidală pentru estimarea materialelor.

Amenajări exterioare și grădinărit

Parcări sau spații pietonale trapezoidale: se estimează suprafața de asfalt sau beton necesar.
Paturi sau straturi cultivate cu margini neparalele pentru optimizarea spațiului și drenaj.

Agricultură și silvicultură

Planificarea parcelelor trapezoidale în hărți cadastrale și calculul suprafeței pentru însămânțare sau reîmpădurire.

Artizanat și meșteșuguri

Croitorii și tâmplarii realizează modele trapezoidale pentru piese de mobilier, covoare sau vitraje, folosind aria pentru tăierea precisă a materialelor.

Formula ariei trapezului

A = ((B + b) × h) / 2

reunește într-o expresie simplă și eficientă toate elementele geometrice relevante: baza mare BBB, baza mică bbb și înălțimea hhh. Prin această formulă putem calcula rapid suprafața oricărui trapez—de la secțiuni de canalizare și suprafețe de vopsit până la parcele agricole și elemente de design interior.

Stăpânirea acestei relații matematice și aplicarea în contexte practice garantează rezultate precise și economii de material, timp și costuri.