Aria triunghiului echilateral – Formula de calcul

Triunghiul echilateral este o figură geometrică fundamentală în matematică, recunoscută pentru simetria și eleganța sa. Este un triunghi cu toate laturile egale ca lungime și toate unghiurile interioare congruente, fiecare măsurând 60 de grade. Această formă simplă, dar perfect echilibrată, este adesea întâlnită atât în geometrie pură, cât și în natură sau arhitectură, datorită stabilității și armoniei pe care o oferă. Studiul triunghiului echilateral ajută la înțelegerea unor concepte importante precum simetria, raporturile între laturi și unghiuri sau proprietățile centrelor geometrice.

Ce este un triunghi echilateral?

Un triunghi echilateral este o figură geometrică plană, clasificată în categoria triunghiurilor regulate. Are trei laturi egale și trei unghiuri interioare identice, fiecare având măsura de 60°. Această egalitate a laturilor și a unghiurilor îi conferă o simetrie aparte, ceea ce îl face unul dintre cele mai studiate tipuri de triunghiuri în matematică.

Triunghiul echilateral este utilizat frecvent în arhitectură, design și natură, datorită echilibrului și stabilității sale. De asemenea, este adesea folosit în demonstrații geometrice și probleme matematice datorită proprietăților sale ușor de recunoscut și de aplicat.

Cum a fost descoperit triunghiul echilateral?

Triunghiul echilateral nu a fost „descoperit” în sensul clasic, ci mai degrabă a fost observat și studiat încă din cele mai vechi timpuri, odată cu dezvoltarea matematicii și a geometriei.

• Apariția în geometria antică – primele civilizații, precum cele din Egipt și Mesopotamia, foloseau forme geometrice simple în construcții și măsurători. Triunghiul echilateral era apreciat pentru simetria și stabilitatea sa, fiind folosit în arhitectură și artă.
• Studiat de grecii antici – matematicienii greci, în special Euclid, au analizat în profunzime triunghiul echilateral. În celebra sa lucrare Elementele, Euclid a demonstrat proprietățile triunghiului echilateral și a construit o metodă geometrică riguroasă pentru trasarea lui cu rigla și compasul.
• Folosit în construcții și simbolistică – triunghiul echilateral a avut și o semnificație simbolică în multe culturi, reprezentând echilibrul, armonia sau divinitatea. În Egiptul antic, unele piramide includ elemente bazate pe forme triunghiulare aproape echilaterale.
• Instrument matematic și filosofic – în filosofia pitagoreică și în școlile geometrice ale Greciei, triunghiul echilateral era considerat o figură „perfectă”, datorită echilibrului complet dintre laturi și unghiuri.

Cum se calculează aria triunghiului?

Aria unui triunghi se poate calcula în mai multe moduri, în funcție de informațiile disponibile. În cazul unui triunghi echilateral, există o formulă specifică, dar mai jos sunt prezentate metodele generale și cea dedicată triunghiului echilateral:

Formule generale pentru orice triunghi:

Cu bază și înălțime: A = (b × h) / 2
unde:
b = lungimea bazei
h = înălțimea corespunzătoare bazei
Cu cele trei laturi (formula lui Heron):
A = √[s × (s – a) × (s – b) × (s – c)]
unde:
a, b, c = laturile triunghiului
s = semiperimetrul = (a + b + c) / 2

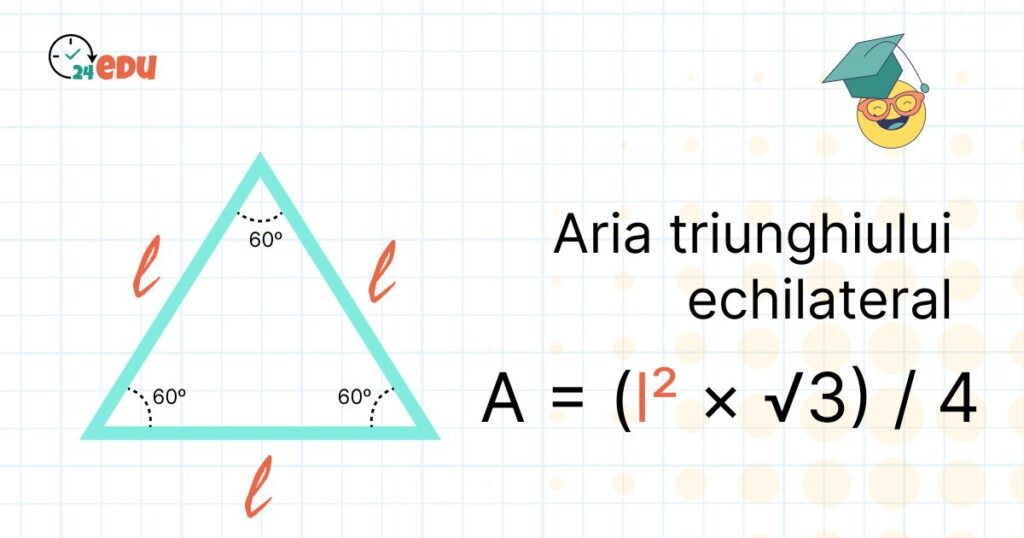
Formulă specială pentru triunghiul echilateral

Dacă știm lungimea laturii l, aria se calculează astfel:

A = (l² × √3) / 4

Această formulă derivă din cea generală, dar ține cont de faptul că toate laturile sunt egale și unghiurile sunt de 60°.

Exemplu pentru triunghi echilateral:

Dacă un triunghi echilateral are latura de 6 cm:

A = (6² × √3) / 4 = (36 × √3) / 4 = 9√3 cm²

Linii folosite la calculul ariei triunghiului echilateral

Pentru a calcula aria unui triunghi echilateral, se folosește înălțimea ca linie principală, dar există și alte linii importante care coincid în cazul acestei forme speciale. 

• Înălțimea – linia trasată dintr-un vârf perpendicular pe latura opusă (baza).
  • Este importantă în calculul ariei, mai ales în formula clasică:
    A = (l × h) / 2
• Mediana – linia care unește un vârf cu mijlocul laturii opuse.
  • În triunghiul echilateral, mediana coincide cu înălțimea.
• Bisectoarea – linia care împarte un unghi în două părți egale.
  • Și aceasta coincide cu înălțimea și mediana.
• Mediatoarea – linia perpendiculară pe o latură, trasată din mijlocul acelei laturi.
  • Coincide cu celelalte linii menționate în triunghiul echilateral.

Așadar, în triunghiul echilateral:

• Toate aceste patru linii sunt una și aceeași pentru fiecare latură.
• Ele se intersectează în același punct – centrul triunghiului, care este și centrul cercului înscris și circumscris.

Proprietățile triunghiului echilateral

Triunghiul echilateral este una dintre cele mai regulate și simetrice figuri geometrice plane. Fiind o formă perfect echilibrată, cu laturi și unghiuri egale, acesta are o serie de proprietăți care îl diferențiază de celelalte tipuri de triunghiuri.

Un triunghi este echilateral dacă toate cele trei laturi au aceeași lungime și toate cele trei unghiuri interioare sunt egale, fiecare măsurând 60 de grade.

Proprietăți:

• Toate laturile sunt egale – lungimea laturilor este identică, ceea ce determină și unghiuri egale.
• Toate unghiurile interioare sunt egale  – fiecare unghi măsoară 60°, deoarece suma unghiurilor într-un triunghi este întotdeauna 180°, iar în acest caz ele se împart în mod egal.
• Toate liniile importante coincid  – în triunghiul echilateral, înălțimile, medianele, mediatoarele și bisectoarele coincid pentru fiecare latură și se intersectează într-un singur punct.
• Are trei axe de simetrie  – fiecare axă trece printr-un vârf și mijlocul laturii opuse. Acest lucru conferă triunghiului echilateral o simetrie perfectă.
• Centrul de greutate, centrul cercului înscris și centrul cercului circumscris coincid  – în alte triunghiuri aceste puncte sunt diferite, dar în triunghiul echilateral ele se suprapun, fiind situate la aceeași distanță față de toate laturile și vârfurile.
• Poate fi înscris și circumscris cu ușurință  – există un cerc care trece prin toate cele trei vârfuri (circumscris) și un cerc care este tangent la toate cele trei laturi (înscris), iar centrul acestor cercuri este același.
• Aria are o formulă specifică  – dacă l este lungimea unei laturi, atunci:
  A = (l² × √3) / 4

Conform MathVox, triunghiul echilateral este adesea folosit în arhitectură, design, logo-uri, și chiar în natură (de exemplu, în structura cristalelor sau a fagurelui de albine). Datorită stabilității și proporțiilor echilibrate, acesta apare frecvent și în problemele de geometrie teoretică.

Greșeli frecvente în calculul ariei triunghiului echilateral

• Confundarea formulei generale cu cea specifică triunghiului echilateral – mulți folosesc greșit formula clasică a ariei unui triunghi (A = (b × h) / 2) fără să cunoască sau să aplice corect înălțimea în cazul echilateralului.
• Calcul greșit al înălțimii  – în triunghiul echilateral, înălțimea nu este egală cu latura. Ea se calculează cu formula:
  h = (l × √3) / 2
  O greșeală des întâlnită este folosirea unei valori greșite sau aproximative pentru această înălțime.
• Neglijarea radicalului din formula ariei  – unii omit radicalul din formula specifică:
  A = (l² × √3) / 4
  și scriu greșit doar A = l² / 4 sau alte variante incomplete.
• Greșeli de rotunjire sau aproximare a lui √3  – când se lucrează cu valori numerice, aproximarea greșită a lui √3 (de exemplu, folosirea 1,7 în loc de 1,732) poate duce la erori semnificative în rezultat.
• Folosirea unei alte formule pentru alt tip de triunghi  – uneori se aplică formule pentru triunghiuri dreptunghice sau isoscele, care nu sunt valabile pentru triunghiul echilateral.
• Ignorarea unităților de măsură  – omisiunea unităților la finalul calculului (cm², m² etc.) sau combinarea incorectă a acestora poate duce la rezultate incomplete sau greșite.

Aceste greșeli pot fi evitate prin înțelegerea clară a proprietăților triunghiului echilateral și aplicarea corectă a formulelor dedicate. Un mic desen ajută adesea la vizualizarea relațiilor corecte dintre elemente.

Unde se aplică aria triunghiului echilateral și de ce este importantă

Calculul ariei triunghiului echilateral are aplicații practice și teoretice în mai multe domenii, datorită formei sale simple și simetrice. 

Aplicații ale ariei triunghiului echilateral:

• În arhitectură și design  – triunghiul echilateral este folosit pentru stabilitate structurală și echilibru estetic. Cunoașterea ariei ajută la estimarea materialelor necesare pentru construcții sau elemente decorative cu formă triunghiulară.
• În matematică și geometrie  – este un exemplu clasic în probleme de arie, simetrie, proporții și demonstrații. Se folosește frecvent în evaluări și concursuri pentru a dezvolta gândirea geometrică.
• În inginerie – triunghiurile echilaterale sunt des întâlnite în structuri precum grinzi, poduri sau cadre metalice, unde aria poate fi folosită pentru calcule legate de greutate, rezistență sau distribuție a forțelor.
• În design grafic și modelare 3D  – triunghiurile sunt elemente de bază în grafica vectorială și modelarea de obiecte. Aria este utilă în calcularea suprafeței totale a unui model sau a unui obiect construit din triunghiuri.
• În natură și biologie  – multe forme naturale, cum ar fi fagurii de albine, folosesc structuri triunghiulare sau hexagonale compuse din triunghiuri echilaterale. Aria este importantă pentru a înțelege eficiența acestor forme.

De ce este importantă aria triunghiului echilateral:

• Oferă o metodă rapidă de măsurare a suprafeței unei forme regulate, fără a fi nevoie să se determine înălțimea separat.
• Simplifică multe probleme geometrice, fiind o figură cu formule dedicate și proprietăți clare.
• Este un exemplu de bază în învățarea geometriei, ajutând la formarea gândirii logice și spațiale.

Teoreme despre triunghiul echilateral – doar enunțurile fără formule

• Toate unghiurile unui triunghi echilateral sunt congruente
  – într-un triunghi echilateral, fiecare unghi interior are aceeași măsură. Aceasta rezultă din faptul că triunghiul are laturile egale, iar într-un triunghi, laturi egale implică și unghiuri opuse egale.
• Toate laturile unui triunghi echilateral sunt egale
  – dacă un triunghi are toate unghiurile egale, atunci și toate laturile sale sunt de aceeași lungime. Aceasta este valabil în ambele sensuri: unghiuri egale implică laturi egale și invers.
• Într-un triunghi echilateral, toate înălțimile, medianele, bisectoarele și mediatoarele coincid
  – spre deosebire de alte triunghiuri, unde aceste linii sunt diferite, în triunghiul echilateral ele sunt una și aceeași pentru fiecare vârf. Acestea se întâlnesc în același punct central.
• Centrul cercului circumscris, centrul cercului înscris și centrul de greutate coincid
  – toate punctele importante asociate triunghiului se află în același loc geometric, în centrul triunghiului. Acesta este un caz rar și unic în geometrie.
• Fiecare înălțime împarte triunghiul echilateral în două triunghiuri congruente
  – trasarea unei înălțimi dintr-un vârf formează două triunghiuri mai mici, identice ca formă și dimensiune. Acest lucru este util în calcule și în demonstrații.
• Triunghiul echilateral are trei axe de simetrie
  – fiecare axă trece printr-un vârf și mijlocul laturii opuse. Aceste axe sunt toate egale și împart triunghiul în părți perfect simetrice.
• Orice triunghi cu trei unghiuri egale este echilateral
  – dacă într-un triunghi toate unghiurile sunt egale, rezultă că și laturile trebuie să fie egale. Acesta este un criteriu pentru recunoașterea triunghiului echilateral.
• Dacă un triunghi are două laturi egale și un unghi de 60°, atunci este echilateral
  – această teoremă arată că dacă deja există două laturi egale și un unghi de 60°, triunghiul nu poate fi decât echilateral, pentru că se impune automat egalitatea tuturor unghiurilor și laturilor.

Curiozități despre triunghiul echilateral

• Este singurul triunghi care este și poligon regulat  – adică are toate laturile și toate unghiurile egale, exact ca pătratul în cazul patrulaterelor.
• Are cele mai multe simetrii dintre toate triunghiurile  – are trei axe de simetrie, în timp ce alte triunghiuri au cel mult una (sau niciuna).
• Toate liniile importante coincid în același punct  – înălțimea, mediana, bisectoarea și mediatoarea trasate din același vârf sunt una și aceeași linie, lucru rar întâlnit în alte triunghiuri.
• Este simbol al echilibrului și al perfecțiunii  – în multe culturi, triunghiul echilateral a fost folosit ca simbol spiritual sau filozofic al armoniei, stabilității și unității.
• Stă la baza structurii hexagonale a fagurelui  – albinele folosesc combinații de triunghiuri echilaterale pentru a forma faguri cu maximă eficiență și rezistență.
• Poate fi trasat doar cu rigla și compasul  – este una dintre primele figuri geometrice pe care elevii o învață să o construiască geometric fără instrumente de măsură.
• Este prezent în logo-uri celebre și design modern  – forma sa echilibrată îl face o alegere populară în branding, arhitectură și design grafic.
• Este auto-similar  – dacă împarți un triunghi echilateral în triunghiuri mai mici, unele dintre ele vor fi tot echilaterale. Această proprietate apare și în formele fractale, precum triunghiul Sierpiński.
• Triunghiul echilateral este folosit în semnalistica rutieră  – de exemplu, semnul „cedează trecerea” este adesea un triunghi echilateral cu vârful în jos, tocmai datorită vizibilității și formei distinctive.

Triunghiul echilateral reprezintă una dintre cele mai armonioase și echilibrate figuri geometrice, remarcându-se prin simetria sa perfectă și proprietățile unice. Prin egalitatea laturilor și a unghiurilor, acesta devine un model ideal pentru înțelegerea conceptelor de bază din geometrie, dar și o sursă de inspirație în artă, arhitectură și natură. Versatilitatea sa îl face nu doar un subiect teoretic important, ci și o formă cu aplicații practice valoroase.