Aria triunghiului isoscel – Formula de calcul

Triunghiul isoscel este o figură geometrică plană, care are două laturi de lungime egală și un unghi cuprins între ele. Această formă este des întâlnită atât în matematică, cât și în viața de zi cu zi, fiind apreciată pentru simetria sa. Într-un triunghi isoscel, unghiurile de la bază sunt egale, iar axa de simetrie trece prin vârful opus bazei, împărțind triunghiul în două părți egale. Proprietățile acestui triunghi stau la baza multor demonstrații geometrice și aplicații practice.

Linii importante în triunghiul isoscel

În triunghiul isoscel, există câteva linii importante care au roluri importante în studiul proprietăților sale. Aceste linii coincid atunci când sunt trase din vârful unghiului format de laturile egale către bază:

• Mediatoarea bazei – este perpendiculara dusă pe bază din mijlocul acesteia.
• Mediana către bază – unește vârful triunghiului cu mijlocul bazei.
• Înălțimea pe bază – este perpendiculara coborâtă din vârf pe bază.
• Bisectoarea unghiului de vârf – împarte unghiul dintre laturile egale în două unghiuri congruente.

Linii importante în triunghiul isoscel

În triunghiul isoscel, există câteva linii importante care au roluri importante în studiul proprietăților sale. Aceste linii coincid atunci când sunt trase din vârful unghiului format de laturile egale către bază:

• Mediatoarea bazei – este perpendiculara dusă pe bază din mijlocul acesteia.
• Mediana către bază – unește vârful triunghiului cu mijlocul bazei.
• Înălțimea pe bază – este perpendiculara coborâtă din vârf pe bază.
• Bisectoarea unghiului de vârf – împarte unghiul dintre laturile egale în două unghiuri congruente.

Cum se calculează aria triunghiului isoscel

Conform CueMath, aria triunghiului isoscel se poate calcula în mai multe moduri, în funcție de datele cunoscute.

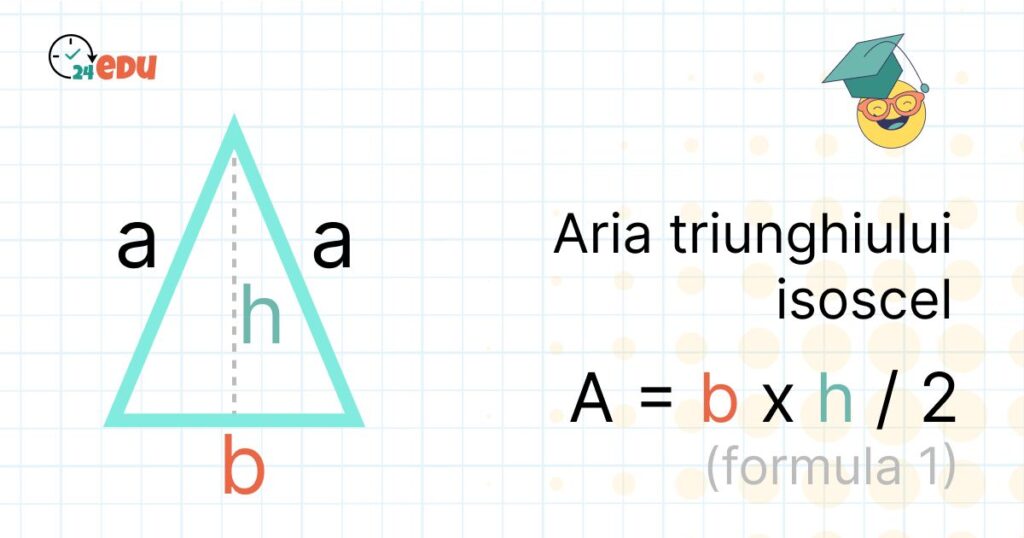
• Dacă se cunoaște baza (b) și înălțimea (h): A = (b × h) / 2
• Dacă se cunosc laturile egale (l) și unghiul dintre ele (A): A = (l² × sin A) / 2
• Dacă se cunosc toate cele trei laturi (b și două laturi egale l): Se poate folosi formula lui Heron: p = (2l + b) / 2 (semiperimetrul) A = √[p(p − l)(p − l)(p − b)]

În majoritatea problemelor, cea mai rapidă metodă este prima, cu baza și înălțimea.

Cele mai frecvente greșeli în calculul ariei unui triunghi isoscel

În calculul ariei unui triunghi isoscel, apar frecvent câteva greșeli tipice, mai ales în rândul elevilor. Iată cele mai comune:

• Confundarea înălțimii cu una dintre laturi – mulți cred că latura egală este înălțimea, deși înălțimea trebuie să fie perpendiculară pe bază.
• Folosirea greșită a formulei – unii aplică formula A = (l × h) / 2, unde l nu este baza, ci una dintre laturile egale, ceea ce duce la un rezultat greșit.
• Neidentificarea corectă a bazei – elevii pot confunda baza cu laturile egale și astfel aplică formula cu valorile inversate.
• Uitarea împărțirii la 2 – în formula A = (b × h) / 2, se uită uneori pasul final: împărțirea produsului la 2.
• Calcul greșit al înălțimii folosind Pitagora – când înălțimea nu e dată, iar elevii o calculează, pot uita să înjumătățească baza pentru a forma triunghiul dreptunghic necesar.
• Folosirea greșită a funcției sinus – dacă se folosește formula A = (l² × sin A) / 2, unghiul trebuie să fie în grade sau radiani corespunzători, altfel rezultatul iese incorect.
• Neglijarea unităților de măsură – se uită uneori conversia între cm, m sau mm, ori se exprimă aria în unități greșite (ex: cm în loc de cm²).

Cine a descoperit triunghiul isoscel – cu multe detalii

Triunghiul isoscel nu a fost „descoperit” în sensul clasic al unei invenții sau al unei descoperiri științifice, ci mai degrabă a fost observat și studiat de-a lungul timpului, încă din Antichitate, ca parte a dezvoltării geometriei.

Civilizațiile antice, precum egiptenii și babilonienii, cunoșteau și foloseau forme triunghiulare în arhitectură, artă și măsurători. Totuși, grecii antici sunt cei care au formalizat studiul triunghiului isoscel.

• Thales din Milet (sec. VI î.Hr.), considerat unul dintre primii matematicieni, este cel care a început să formuleze primele teoreme geometrice, printre care și proprietăți legate de triunghiuri. Se crede că el a fost printre primii care au observat că unghiurile de la bază ale unui triunghi isoscel sunt egale.
• Pitagora și școala sa au continuat studiul triunghiurilor, mai ales al celor isoscele și dreptunghice, demonstrând proprietăți importante precum simetria și relațiile dintre laturi și unghiuri.
• Euclid (circa 300 î.Hr.), în lucrarea sa faimoasă Elementele, a inclus mai multe propoziții și demonstrații despre triunghiurile isoscele. În Cartea I, Propoziția 5 (numită și „teorema măgărușului”), Euclid demonstrează riguros că într-un triunghi isoscel, unghiurile de la bază sunt egale. Această teoremă este considerată una dintre cele mai vechi și importante legate de triunghiuri.

De-a lungul timpului, triunghiul isoscel a devenit un element fundamental în geometrie, folosit nu doar în teorie, ci și în construcții, arhitectură, desen tehnic și chiar artă. Prin simetria și simplitatea sa, a atras atenția multor gânditori și matematicieni, fiind unul dintre cele mai studiate tipuri de triunghiuri.

Cine a fost Thales din Milet (sec. VI î.Hr.)

Thales din Milet a fost un filosof, matematician și astronom grec din secolul al VI-lea î.Hr., considerat de mulți ca fiind părintele științei și al geometriei occidentale. A trăit în orașul Milet, situat în Asia Mică (astăzi în Turcia), și a fost una dintre cele mai importante figuri ale lumii antice.

Ce a făcut Thales și de ce este important:

• A introdus raționamentul logic în matematică – Thales a fost printre primii care au încercat să explice lumea prin rațiune, nu prin mituri sau legende. A pus bazele demonstrării geometriei folosind deducția logică.
  
• A studiat triunghiurile – i se atribuie mai multe teoreme geometrice, precum:
  
  • Unghiurile de la bază ale unui triunghi isoscel sunt egale
    
  • Dacă un triunghi este înscris într-un cerc și are ca latură un diametru, atunci este dreptunghic (cunoscută azi ca teorema lui Thales)
    
• A măsurat înălțimea piramidelor – se spune că Thales a folosit umbrele și proporțiile triunghiurilor pentru a calcula înălțimea unei piramide din Egipt, ceea ce arată că aplica cunoștințele geometrice în mod practic.
  
• A fost interesat de astronomie – ar fi prezis o eclipsă de Soare (probabil în 585 î.Hr.), ceea ce l-a făcut celebru în lumea greacă.
  
• A fost considerat unul dintre Cei Șapte Înțelepți ai Greciei – o distincție dată celor mai înțelepți oameni ai vremii.

Thales nu a lăsat lucrări scrise care să fi supraviețuit, dar ideile și contribuțiile sale au fost transmise prin scrierile altor gânditori, precum Aristotel. A fost un pionier al gândirii științifice, punând bazele unei tradiții intelectuale care avea să influențeze toată cultura occidentală.

Cine a fost Pitagora?

Pitagora a fost un filosof și matematician grec care a trăit în secolul al VI-lea î.Hr., cunoscut mai ales pentru celebra teoremă care îi poartă numele, dar și pentru contribuțiile sale în filozofie, muzică, astronomie și educație. S-a născut în insula Samos și a călătorit mult, inclusiv în Egipt și Babilon, pentru a învăța de la alte culturi.

Ce l-a făcut faimos:

• Teorema lui Pitagora – într-un triunghi dreptunghic, pătratul ipotenuzei este egal cu suma pătratelor catetelor: c² = a² + b² Deși această relație era cunoscută și de alte civilizații (egipteni, babilonieni), Pitagora și școala sa sunt cei care au oferit prima demonstrație logică a acesteia.
• A fondat o școală filozofico-matematică – numită Școala pitagoreică, era o comunitate aproape religioasă, cu reguli stricte, unde se credea că numerele sunt esența întregului univers.
• A studiat armonia muzicală – a descoperit că raporturile numerice simple (1:2, 2:3 etc.) între lungimile corzilor produc sunete armonioase, legând astfel matematica de muzică.
• A influențat filosofia – Pitagora a fost printre primii care au vorbit despre nemurirea sufletului și despre reîncarnare. Școala sa promova purificarea sufletului prin cunoaștere, muzică și viață morală.
• A avut o viziune matematică asupra lumii – pitagoreicii credeau că totul poate fi explicat prin numere și proporții. Această idee a pus bazele unei tradiții care a marcat gândirea științifică europeană timp de secole.

Alte curiozități:

• Membrii școlii pitagoreice nu aveau voie să mănânce fasole.
• Pitagora este înconjurat de multe legende, iar istoricii nu pot confirma toate realizările atribuite lui personal – multe dintre ele vin de la discipolii săi.

Pitagora rămâne una dintre cele mai influente figuri ale Antichității, nu doar pentru matematică, ci și pentru modul în care a unit gândirea logică cu filozofia, arta și spiritualitatea.

Proprietățile triunghiului isoscel

Triunghiul isoscel are o serie de proprietăți geometrice clare, care îl deosebesc de celelalte tipuri de triunghiuri.

• Două laturi sunt egale – laturile care formează unghiul de vârf au aceeași lungime.
• Unghiurile de la bază sunt egale – unghiurile opuse laturilor egale au aceeași măsură.
• Axa de simetrie trece prin vârful triunghiului și mijlocul bazei – triunghiul este simetric față de această axă.
• Înălțimea, mediana, bisectoarea și mediatoarea trase din vârf coincid – toate aceste linii sunt una și aceeași în triunghiul isoscel.
• Împărțirea triunghiului în două triunghiuri dreptunghice egale – dacă se trasează înălțimea din vârf pe bază, rezultă două triunghiuri congruente.
• Are un singur unghi diferit – unghiul de vârf este diferit de cele de la bază, dacă triunghiul nu este echilateral.
• Perimetrul și aria pot fi calculate ușor – datorită simetriei, formulele devin mai simple când se cunosc latura și baza.

Teoreme legate de triunghiul isoscel

• Într-un triunghi isoscel, unghiurile de la bază sunt egale – Dacă două laturi sunt egale, atunci unghiurile opuse acestora sunt și ele egale.
• Reciproca: dacă două unghiuri ale unui triunghi sunt egale, atunci triunghiul este isoscel – Egalitatea unghiurilor implică și egalitatea laturilor opuse lor.
• Într-un triunghi isoscel, înălțimea din vârf este și mediana, și bisectoare, și mediatoare pe bază – Această linie împarte triunghiul în două triunghiuri dreptunghice congruente.
• Teorema unghiului exterior – În orice triunghi, un unghi exterior este egal cu suma unghiurilor interioare neadiacente. În triunghiul isoscel, dacă unul dintre aceste unghiuri e de la bază, putem afla rapid unghiul exterior.
• Teorema lui Euclid (Propoziția 5 din Elementele) – Într-un triunghi isoscel, dreapta trasată din vârful unghiului format de laturile egale către mijlocul bazei este perpendiculară pe bază și îl împarte în două triunghiuri congruente.

Aplicații ale triunghiului isoscel

Triunghiul isoscel are multe aplicații practice datorită simetriei și proprietăților sale geometrice.

• În arhitectură – Este folosit pentru stabilitate și estetică în construcții. Acoperișurile în formă de „A” sunt adesea triunghiuri isoscele, pentru a distribui greutatea uniform.
• În inginerie – Se folosește la proiectarea structurilor de susținere, cum ar fi grinzi și poduri, unde simetria ajută la echilibrarea forțelor.
• În artă și design – Simetria triunghiului isoscel este apreciată în compoziții vizuale, pictură, sculptură sau design grafic, oferind un sentiment de echilibru și armonie.
• În navigație și topografie – Este folosit în trilaterare, pentru a determina poziții sau distanțe necunoscute, bazându-se pe unghiuri și laturi cunoscute.
• În construcția de instrumente optice – Prismele isoscele sunt folosite în unele sisteme optice pentru reflectarea sau devierea luminii la unghiuri precise.
• În educație – Este un exemplu simplu și clar pentru predarea conceptelor de simetrie, congruență, unghiuri și laturi egale.

Curiozități despre triunghiul isoscel

• Este triunghiul cel mai des folosit în arhitectură – Datorită stabilității și simetriei sale, se regăsește în acoperișuri, frontoane și structuri de susținere.
• Poate fi și dreptunghic și isoscel în același timp – Dacă are un unghi de 90° și celelalte două laturi egale, este un triunghi isoscel dreptunghic – folosit frecvent în construcții.
• Este singurul triunghi în care patru linii importante coincid – înălțimea, mediana, bisectoarea și mediatoarea trase din vârf sunt aceeași linie, unică pentru triunghiul isoscel.
• Simbol al echilibrului și armoniei – în multe culturi, forma triunghiului isoscel este asociată cu stabilitatea și ordine universală, fiind folosită și în simboluri religioase sau mistice.
• Se regăsește în natură – Aripile unor insecte, structura fulgilor de nea sau vârfurile munților au deseori formă apropiată de triunghi isoscel.
• Ajută în identificarea greșelilor în desen – În problemele de geometrie, dacă un triunghi declarat isoscel nu are unghiurile de la bază egale, atunci desenul este incorect.

Cum poți învăța copiii mai ușor despre triunghiul isoscel

Pentru a-i ajuta pe copii să învețe mai ușor despre triunghiul isoscel, e important să folosești metode vizuale, practice și interactive:

• Desene și decupaje – copiii pot decupa triunghiuri din hârtie colorată și le pot plia pentru a observa simetria și egalitatea unghiurilor și a laturilor.
• Exemple din viața reală – arată-le triunghiuri isoscele în obiecte din jur: acoperișuri, semne de circulație, decorațiuni, instrumente muzicale etc.
• Construcții cu bețișoare sau paie – lăsându-i să formeze singuri triunghiuri cu laturi egale, vor înțelege mai bine structura lor.
• Desene pe tablă interactivă sau aplicații educaționale – există jocuri și aplicații care le permit să creeze și să modifice triunghiuri digital.
• Povești și personaje – inventează o poveste cu un „triunghi isoscel curajos” care salvează alte forme geometrice folosindu-și simetria și stabilitatea.
• Experimente cu oglinzi – așază o oglindă pe bază pentru a arăta cum triunghiul este simetric și cum se reflectă perfect de o parte și de alta.

Triunghiul isoscel este o figură geometrică importantă, apreciată pentru simplitatea și simetria sa. Prin proprietățile sale unice – precum egalitatea laturilor și a unghiurilor de la bază – devine un element fundamental în studiul geometriei, dar și în aplicații practice din arhitectură, inginerie sau artă. Prezent atât în teorie, cât și în realitate, triunghiul isoscel rămâne un exemplu clar al modului în care formele simple pot avea semnificații profunde și utilizări diverse.