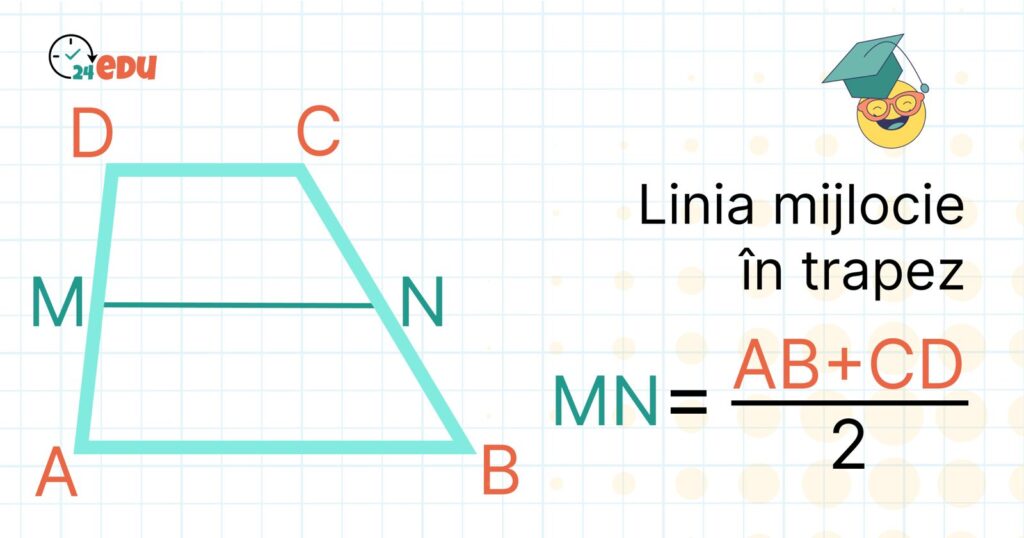
Linia mijlocie în trapez - Cum se calculează

Geometria clasei a VII-a este interesantă, dar în același timp și dificilă, deoarece apar multe noțiuni noi și complexe. Însă, acestea pot fi mai ușoare dacă le înțelegi într-un mod logic și exersezi apoi ce ai învățat.

Astăzi vrem să vorbim despre trapez, mai exact despre linia mijlocie în trapez, o noțiune care o să vezi că va fi destul de simplă.

Înainte însă, vrem să îți vorbim puțin despre trapez.

Ce este un trapez

Un trapez este o figură geometrică cu patru laturi, adică un patrulater. Ce îl face special față de alte patrulatere este că are două laturi opuse care sunt paralele, iar celelalte două nu sunt paralele, așa cum ne spune și Cuemath.

Laturile care sunt paralele se numesc baze – avem o bază mare (cea mai lungă) și o bază mică (cea mai scurtă). Laturile care nu sunt paralele se numesc laturi oblice.

Trapezele nu sunt toate la fel. Ele se împart în trei tipuri, în funcție de forma lor și de cum arată laturile și unghiurile.

trapez dreptunghic – are un unghi drept (adică de 90°). Uneori poate avea chiar două unghiuri drepte, unul lângă fiecare bază.
trapez isoscel – are laturile oblice egale (adică cele două laturi care nu sunt paralele au aceeași lungime). În plus, unghiurile de lângă baza mare sunt egale.
trapez oarecare – este cel mai obișnuit tip. Are doar cele două baze paralele, dar nicio altă regulă specială. Laturile oblice nu sunt egale, nici unghiurile.

Trapezul este un patrulater special, recunoscut prin faptul că are două laturi opuse paralele, numite baze. Deși toate trapezele au această trăsătură comună, ele pot arăta diferit în funcție de lungimea laturilor și mărimea unghiurilor.

Linia mijlocie în trapez – definiție și termeni

În orice trapez există o linie mijlocie foarte importantă, pe care o vei întâlni frecvent în problemele de geometrie. Aceasta este un segment care unește mijloacele laturilor trapezului care nu sunt paralele și are următoarea formulă:

MN = AB + CD2

Pentru a-ți fi totul cât mai clar vom lua un exemplu:

ABCD = trapez;
AB ॥ CD;
M = mijlocul laturii AD (⇒ două segmente congruente: AM = MD);
N = mijlocul laturii BC (⇒ două segmente congruente: BN = NC).

Dacă unim M cu N cu ajutorul unui segment, respectivul segment este linia mijocie din trapez.

Am folosit câțiva termeni care este posibil să te încurce puțin în cazul în care nu ți-i mai amintești, motiv pentru care vrem să ți-i definim:

segment – acest termen face referire la o linie dreaptă care are două capete bine stabilite;
paralele – aici ne referim la două linii drepte, care pot merge împreună la infinit și nu se vor întâlni niciodată;
congruente – termenul acesta face referire la două figuri geometrice au aceeași formă și mărime.

Proprietățile liniei mijlocii în trapez

Linia mijlocie într-un trapez vine cu multe proprietăți, iar dacă le știi, îți va fi mult mai ușor să rezolvi unele exerciții.

este unică, deoarece fiecare latură are un singur punct aflat la mijloc

Linia mijlocie în trapez este o dreaptă unică, deoarece orice latură a trapezului poate avea un singur punct aflat pe mijloc. Prin unirea a două puncte de pe laturi oblice, mai exact cele care nu sunt paralele, se obține o singură linie – linia mijlocie.

În desenul nostru avem două laturi oblice, AD și BC. După ce am identificat mijlocul acestora, am notat cu M punctul de mijloc al laturii AD și cu N cel al laturii BC. Apoi, trasând o linie din punctul M în punctul N, am obținut linia mijlocie a trapezului.

este paralelă cu bazele

Spunem că linia mijlocie este paralelă cu bazele, nu cu baza, deoarece că trapezul are două baze, cea mare și cea mică. Le putem identifica foarte simplu, deoarece ele sunt vizibile. În cazul prezentat de noi, AB este baza mică, iar CD este baza mare.

Aceste două linii nu se vor intersecta niciodată, oricât de lungi ar fi. Mai mult decât atât, linia mijlocie trasată de noi, MN, este și ea paralelă cu aceste două baze.

Prin urmare, dacă linia mijlocie este paralelă cu una dintre baze, automat va fi paralelă și cu cealaltă ⇒ AB ॥ CD ॥ MN

ne poate ajuta să demonstrăm paralelismul

Dacă într-o problemă de geometrie ți se spune că un punct este la mijlocul unei laturi oblice și că linia trasată prin acel punct este paralelă cu una dintre baze, atunci poți spune că este vorba despre linia mijlocie.

Și pentru că linia mijlocie este mereu paralelă cu ambele baze, automat rezultă că este paralelă și cu cealaltă bază. Această informație te ajută să demonstrezi paralelismul în exerciții, fără să mai fie nevoie să calculezi unghiuri sau să faci alte demonstrații complicate.

poate forma unghiuri congruente și suplimentare

Linia mijlocie în trapez duce la formarea unor unghiuri congruente și suplimentare, deoarece există două drepte paralele tăiate de o secantă. Prin urmare:

∢ M și ∢ D sunt congruente, aflându-se de aceeași parte a secantei;
∢ N și ∢ C sunt congruente, aflându-se de aceeași parte a secantei.
∢ M, ∢ D, ∢ N și ∢ C sunt toate congruente doar atunci când este vorba de un trapez isoscel.
are o formulă foarte simplă

Formula de calcul pentru lungimea liniei mijlocii din trapez este media aritmetică dintre cele două baze sau semisuma bazelor și are formula: MN = AB + CD2.

Prin urmare, ce trebuie să faci pentru a-i afla lungimea este sa calculezi cât însumează cele două laturi și să împarți totul la 2.

Iată și un exemplu:

AB = 10 cm
CD = 6 cm
MN = ?

MN = 10 + 62 = 162 = 8 cm

Cum ne ajută în matematică linia mijlocie în trapez

Linia mijlocie este foarte utilă în matematică, mai ales în problemele de geometrie. Iată cum:

simplifică calculele – cu ajutorul formulei liniei mijlocii, putem găsi rapid lungimea ei, fără să măsurăm nimic. Dacă știm lungimea bazelor, e de-ajuns să facem media aritmetică (adică le adunăm și împărțim la 2).
ajută la demonstrații – în probleme în care trebuie să arătăm că două linii sunt paralele, linia mijlocie ne oferă o scurtătură. Dacă știm că unește mijloacele laturilor oblice și e paralelă cu o bază, atunci știm sigur că e paralelă și cu cealaltă. Așa putem demonstra mai ușor paralelismul în trapez.
ajută să înțelegem mai bine formele geometrice – când desenăm linia mijlocie, trapezul pare împărțit în două părți mai ușor de analizat. Uneori, putem transforma un trapez în două triunghiuri sau în figuri mai simple, cu care deja suntem obișnuiți.
se folosește și pentru calculul ariei trapezului – chiar dacă aria trapezului are formula sa proprie, linia mijlocie apare și acolo. Având în vedere că Aria trapezului = lungimea liniei mijlocii x înălțimea, dacă știm linia mijlocie și înălțimea, putem afla imediat suprafața trapezului.
ne învață să observăm relații între elemente – geometria nu înseamnă doar măsurători, ci și gândire logică. Linia mijlocie arată cum elementele unei figuri sunt legate între ele: paralele, egale, mijlocii.

Linia mijlocie în trapez – aplicații în viața reală

Poate te întrebi: „La ce îmi folosește mie linia mijlocie în afara orei de mate?” Ei bine, geometria, și mai ales linia mijlocie din trapez, apare mai des decât crezi în lucrurile din jurul nostru.

în construcția drumurilor, rampelor și podurilor – inginerii folosesc trapeze atunci când proiectează rampe sau poduri înclinate. Linia mijlocie îi ajută să calculeze lungimi, înălțimi și puncte de echilibru.
la realizarea acoperișurilor – unele acoperișuri au forma unui trapez. Linia mijlocie poate indica punctul de sprijin sau ajută la calculul dimensiunii lemnului necesar pentru construcție.
în desen tehnic și arhitectură – trapezele apar des în planuri de clădiri sau în desenul de perspectivă. Linia mijlocie e utilă pentru trasarea corectă a formelor și pentru obținerea proporțiilor corecte.
la proiectarea mobilei sau a obiectelor – când se construiesc mese, rafturi sau scaune cu laturi înclinate, trapezul poate apărea în proiect. Linia mijlocie ajută la calculul dimensiunilor și la poziționarea corectă a pieselor.
în fațadele clădirilor moderne – ferestrele sau panourile trapezoidale sunt folosite în arhitectura contemporană. Linia mijlocie ajută la stabilirea centrului și la împărțirea simetrică a spațiului.

Linia mijlocie nu este doar ceva ce vei învăța doar pentru teste. Ea este folosită în meserii importante, precum arhitectura, ingineria sau designul. Dacă înveți să o înțelegi și să o aplici, vei putea să o recunoști peste tot în jurul tău.

La ce să fii atent atunci când calculezi linia mijlocie în trapez

Când rezolvi o problemă și trebuie să calculezi linia mijlocie, e important să nu te grăbești. Uite ce trebuie să verifici:

asigură-te că ai de-a face cu un trapez – verifică dacă două dintre laturile opuse sunt paralele. Doar atunci putem vorbi despre baze și linie mijlocie.
identifică bazele în mod corect – baza mare și baza mică sunt laturile paralele. Uneori pot fi scrise cu litere diferite (de exemplu, AB și CD). Nu le încurca cu laturile oblice!
folosește corect formula – linia mijlocie se calculează cu ajutorul formulei: MN = AB + CD2. Mai exact, dacă adică aduni lungimile celor două baze și împarți rezultatul la 2, obții linia mijlocie în trapez.
folosește aceleași unități de măsură – dacă o bază este în centimetri și cealaltă în milimetri, trebuie să le transformi mai întâi în aceeași unitate.
fii atent la cerință – uneori nu ți se cere să calculezi linia mijlocie, ci să o folosești pentru a afla altceva (de exemplu, înălțimea sau aria trapezului).
nu confunda linia mijlocie cu o altă latură – linia mijlocie nu este niciodată o bază, nici o latură oblică. Este segmentul care unește mijloacele laturilor oblice.
verifică dacă se cere doar lungimea sau și justificarea – dacă problema este de tip demonstrație, trebuie să explici de ce segmentul este linia mijlocie (de exemplu, că unește mijloacele laturilor oblice și e paralel cu baza).

Fă întotdeauna un desen simplu, cu literele trecute corect pe laturi. Te va ajuta să nu te încurci și să aplici formula fără greșeli.

Cum să înveți mai ușor noțiuni de geometrie

Geometria nu trebuie să fie grea sau plictisitoare. Dacă înveți cu răbdare și înțelegi ce faci, totul devine mult mai simplu. Iată câteva sfaturi care te pot ajuta:

desenează mereu figurile – geometria e o materie care „se vede”. Când citești un exercițiu, fă imediat un desen. Nu trebuie să fie perfect, dar te ajută enorm să înțelegi ce se întâmplă.
folosește culori diferite – când înveți sau când faci un desen, folosește creioane colorate. Cu roșu marchezi unghiurile, cu albastru laturile egale, cu verde linia mijlocie… așa ții mai bine minte!
învață noțiunile pe rând – nu te grăbi să sari de la un trapez la un cerc, apoi la triunghiuri. Fiecare figură are regulile ei. Încearcă să înțelegi bine o figură înainte de a trece la alta.
reține cuvintele importante – notează-ți undeva termenii cheie: segment, paralel, congruent, perpendicular, medie aritmetică etc. Și scrie lângă ei explicații simple, așa cum le-ai spune unui prieten.
fă legături cu lucruri din viața reală – trapezul poate fi o rampă, un acoperiș, o masă cu picioare înclinate. Când legi geometria de lumea reală, o înțelegi mai ușor și o ții minte mai bine.
rezolvă câte puțin în fiecare zi – nu lăsa totul pe ultima zi. Mai bine faci 10 minute de geometrie în fiecare zi, decât 2 ore înainte de test. E ca la sport – cu antrenament ușor, dar constant, devii mai bun.
întreabă atunci când nu înțelegi – nu e rușinos să întrebi, ba din contră, e o dovadă că vrei să înveți. Poți întreba un coleg, un profesor sau chiar pe cineva ca mine, care e aici să te ajute.

Geometria nu e despre note sau formule recitate pe de rost. E despre a înțelege cum funcționează spațiul din jurul tău. Dacă înveți cu mintea deschisă și cu un strop de curiozitate, totul devine mai ușor și chiar distractiv.

Linia mijlocie din trapez nu este doar o linie trasată între două puncte. Este o unealtă importantă, care ne ajută să înțelegem mai bine figurile geometrice, să facem calcule mai rapide și să demonstrăm relații între laturi și unghiuri.

Cu o formulă simplă și proprietăți logice, linia mijlocie este un instrument util care îți arată cum funcționează lucrurile într-un trapez și te ajută să vezi legăturile dintre laturi și unghiuri.

Linia mijlocie în trapez – Cum se calculează