Cercul este una dintre cele mai simple și totodată fascinante figuri geometrice, prezentă pretutindeni în natură și în creațiile umane. Îl întâlnim în forma Soarelui și a Lunii pe cer, în roțile vehiculelor, în ceasuri și chiar în planurile de arhitectură ale clădirilor. Studiul proprietăților cercului este important în geometrie, iar una dintre caracteristicile sale fundamentale este lungimea cercului, cunoscută și sub numele de circumferință.
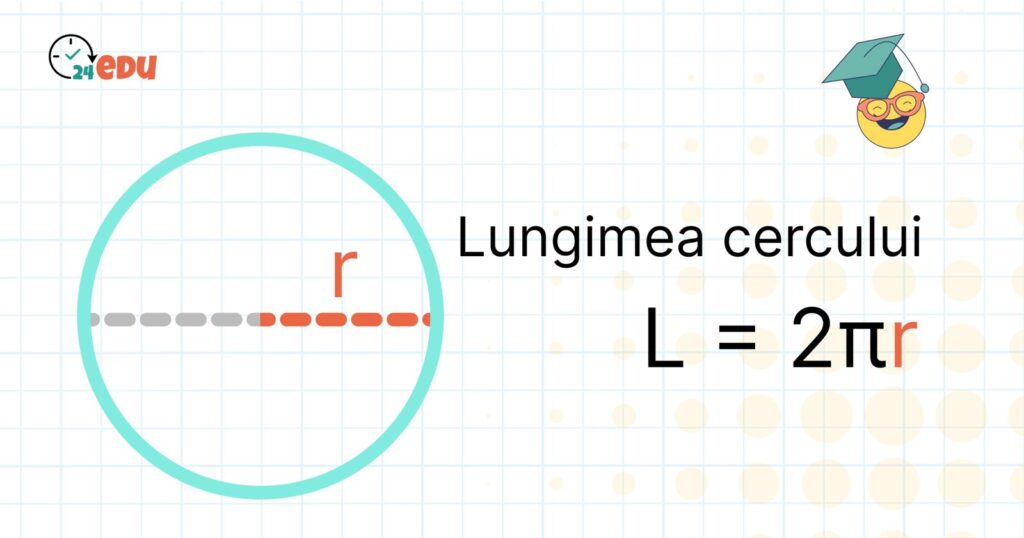
Lungimea cercului reprezintă distanța totală pe care am parcurge-o dacă am înconjura o dată întreaga linie a cercului. Această mărime are o importanță practică uriașă: ne ajută să calculăm câți metri are o pistă circulară, cât material este necesar pentru a face un cadru rotund sau chiar câte rotații trebuie să facă o roată pentru a parcurge o anumită distanță.
2. Elemente ale cercului
Conform, Math is fun, pentru a înțelege cum se calculează lungimea cercului, este important să analizăm mai întâi elementele sale fundamentale. Cercul este definit ca locul geometric al tuturor punctelor dintr-un plan aflate la aceeași distanță de un punct fix numit centru. Această simplitate ascunde o eleganță matematică ce stă la baza multor proprietăți interesante.
Raza (r)
Raza cercului este segmentul care unește centrul cercului cu orice punct de pe linia sa. Este una dintre cele mai importante mărimi geometrice, deoarece lungimea cercului și aria suprafeței delimitate depind direct de valoarea ei. Toate razele unui cerc sunt egale.
Exemplu: dacă punctul central al cercului este notat cu O, iar un punct pe contur este A, segmentul OA este raza.
Diametrul (d)
Diametrul este segmentul care unește două puncte opuse ale cercului și trece prin centrul acestuia. Este de două ori mai mare decât raza:
Diametrul este de două ori raza:
d = 2r
Exemplu: Dacă raza cercului este 5 cm, diametrul va fi 10 cm.
Diametrul joacă un rol important în formula lungimii cercului.

Relevanța acestor elemente
Cunoașterea razei, diametrului și a constantei π\piπ ne permite să derivăm formula lungimii cercului și să înțelegem modul în care aceste mărimi se raportează între ele.
3. Definirea lungimii cercului
Lungimea cercului, denumită adesea circumferință, este distanța totală pe care o parcurgem dacă înconjurăm o dată conturul cercului. Ea reprezintă măsura „perimetrului” pentru figura rotundă și este o noțiune de bază în geometria plană.
Raportul dintre lungime și diametru
Cel mai important rezultat legat de lungimea cercului este faptul că pentru orice cerc:
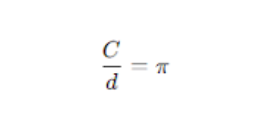
unde:
- C este lungimea cercului (circumferința)
- d este diametrul.
Acest raport constant, egal cu π\piπ, ne arată că lungimea cercului crește proporțional cu diametrul său.
Legătura cu raza
Folosind relația d=2rd = 2rd=2r, putem exprima circumferința și în funcție de raza cercului:
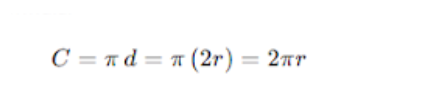
Astfel, pentru a calcula lungimea cercului, este suficient să cunoaștem raza și să aplicăm formula de mai sus.
Analogii vizuale
- „Desfășurarea” conturului: Gândește-te la conturul cercului ca la un inel de cauciuc. Dacă tai acel inel și îl întinzi într-o linie dreaptă, lungimea acelei linii corespunde circumferinței inițiale.
- Fir în jurul unui obiect: Dacă ai un fir și îl fixezi la un punct de pe cerc, apoi îl întinzi complet în jurul cercului și îl taie la același punct de pornire, lungimea firului tăiat este exact C.
4. Formula lungimii cercului
Pentru a stabili formula exactă care leagă lungimea cercului de raza sa, pornim de la raportul fundamental

Demonstrație intuitivă
- Raportul constant
- Măsurând lungimea mai multor cercuri de raze diferite și împărțind-o la diametrul fiecăruia, obținem întotdeauna aceeași valoare, π\piπ.
5. Exemple de calcul
Exemplul 1: Cerc cu rază în centimetri

Rezultat: aproximativ 25.13 cm.
Exemplul 2: Conversie între unități

Rezultat: 1.57 m sau 157.08 cm.
Exemplul 3: Pistă de alergare

Rezultat: un tur măsoară aproximativ 229.4 m.
6. Aplicații practice
Lungimea cercului, C=2πrC = 2\pi rC=2πr, este un instrument de bază în multe domenii:
- Arhitectură și design:
- Ferronneriile rotunde, ferestrele circulare sau balustradele curbate sunt proiectate folosind lungimea arcului.
- Covețele decorative și ornamentele circulare necesită calcularea precisă a materialului necesar pentru a acoperi circumferința.
- Inginerie și construcții:
- Pentru instalarea conductelor (țevi) se măsoară lungimea exterioară a secțiunii circulare pentru a estima cantitatea de material izolant sau de acoperire.
- Proiectele de drumuri circulare (rondouri, giratorii) depind de lungimea arcului pentru trasarea benzilor de circulație.
- Transport și mecanică:
- În automobile și ciclism, diametrul și circumferința roților determină raportul de transmisie și viteza la o rotație completă.
- Rolele și tamburii cilindrici folosesc lungimea cercului pentru calculul frecării și al tensiunii în curele.
- Producție și ambalare:
- Etichetele cilindrice de pe sticle, conserve sau cilindri industriali se proiectează pe baza circumferinței.
- Benzile transportoare rotunde necesită calcularea lungimii conturului roții pentru înlocuirea corectă a benzilor.
- Viața cotidiană:
- Foaia rotundă de pizza sau tort necesită cunoașterea circumferinței pentru a tăia felii egale.
- Benzile de cauciuc folosite ca garnituri o-ring în mecanisme se cumpără în lungime, calculată după diametrul interior.
Formula lungimii cercului, C = 2 * pi * r, sintetizează o proporționalitate directă între dimensiunea geometrică de bază (raza) și măsura perimetrului. Am explorat definirea corectă a elementelor cercului — raza, diametrul și constanta π —, am derivat formula pas cu pas și am ilustrat aplicabilitatea ei prin exemple și probleme concrete.
În viața reală, de la proiecte de arhitectură și inginerie până la activități casnice și hobby-uri, măsurarea circumferinței cercurilor este indispensabilă. Prin însușirea acestei relații simple, cititorul dobândește o abilitate utilă pentru rezolvarea rapidă și precisă a problemelor ce implică geometria curbilinie.

Leave a Reply