Piramidele reprezintă o clasă importantă de corpuri geometrice studiate atât în matematică, cât și în arhitectură și inginerie. Ele au atras atenția încă din Antichitate, fiind folosite în construcții monumentale, cum ar fi piramidele egiptene. În geometria spațială, o piramidă este definită ca un poliedru cu o bază poligonală și fețe laterale triunghiulare care se întâlnesc într-un singur punct numit vârf.

Importanța piramidei triunghiulare regulate în geometrie
Dintre toate tipurile de piramide, piramida triunghiulară regulată este una dintre cele mai simple și elegante forme tridimensionale. Ea are o bază triunghi echilateral și trei fețe laterale congruente, fiecare fiind un triunghi isoscel. Studiul acestui corp geometric este important pentru înțelegerea proprietăților volumetrice, a secțiunilor plane și a simetriilor spațiale. În plus, piramida triunghiulară regulată stă la baza construirii și înțelegerii altor poliedre mai complexe.
2. Definirea piramidei triunghiulare regulate
Elemente componente ale unei piramide
O piramidă este un poliedru format dintr-o bază poligonală și fețe laterale triunghiulare care se întâlnesc într-un punct comun numit vârf. În cazul unei piramide triunghiulare, baza este un triunghi, iar fețele laterale sunt trei triunghiuri care au laturi comune cu baza și se unesc într-un vârf.
Piramida triunghiulară regulată are următoarele elemente:
- Baza: un triunghi echilateral, adică un triunghi cu toate laturile și unghiurile egale.
- Fețele laterale: trei triunghiuri isoscele congruente, cu baza comună cu laturile triunghiului echilateral și vârfurile unite în punctul superior.
- Muchiile: șase în total – trei muchii ale bazei și trei muchii laterale care pornesc din fiecare vârf al bazei spre vârful piramidei.
- Vârfurile: patru în total – cele trei ale bazei și vârful piramidei.
Particularități ale bazei triunghiulare regulate
Baza piramidei triunghiulare regulate este importantă în determinarea proprietăților corpului:
- Laturile triunghiului echilateral se notează cu aaa.
- Înălțimea bazei (h_b), adică distanța de la un vârf al triunghiului la mijlocul laturii opuse, este:
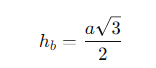
unde:
- a = latura triunghiului echilateral,
- hb = înălțimea triunghiului echilateral (distanța de la un vârf la mijlocul laturii opuse).
Reprezentarea grafică și notarea
Pentru a descrie clar piramida triunghiulară regulată, folosim următoarea notare:
- Baza este triunghiul ABC, cu vârfurile în planul bazei.
- Vârful piramidei este notat S, situat deasupra centrului bazei.
- Muchiile laterale sunt segmentele SA,SB,SCSA, SB, SCSA,SB,SC, iar fețele laterale sunt triunghiurile SAB,SBC,SCASAB, SBC, SCASAB,SBC,SCA.
Într-o reprezentare 3D, centrul bazei O este punctul în care înălțimea piramidei, SO, cade perpendicular pe planul triunghiului ABC.
Definiția formală
Piramida triunghiulară regulată este un poliedru format dintr-o bază triunghi echilateral și trei fețe laterale triunghiuri isoscele congruente, care au un vârf comun situat pe o perpendiculară pe planul bazei, trasată prin centrul acesteia.
3. Proprietăți geometrice
Muchii, vârfuri și fețe
Piramida triunghiulară regulată are o structură simplă, dar elegantă:
- Muchii: sunt în total 6 muchii – 3 muchii ale bazei (AB,BC,CAAB, BC, CAAB,BC,CA) și 3 muchii laterale (SA,SB,SCSA, SB, SCSA,SB,SC), care unesc vârful piramidei SSS cu fiecare vârf al bazei.
- Vârfuri: 4 în total – cele 3 vârfuri ale bazei (A,B,CA, B, CA,B,C) și vârful piramidei SSS.
- Fețe: 4 fețe – baza triunghiulară (ABCABCABC) și cele 3 fețe laterale triunghiulare (SAB,SBC,SCASAB, SBC, SCASAB,SBC,SCA).
Axe de simetrie și planuri de simetrie
Datorită configurației regulate, piramida prezintă multiple simetrii:
- Axe de simetrie: există 3 axe de simetrie care trec prin vârful piramidei SSS și mijlocul fiecărei laturi a bazei.
- Planuri de simetrie: fiecare axă de simetrie se află într-un plan de simetrie, care taie piramida în două părți congruente.
- Simetrie centrală: punctul OOO, centrul bazei, este punctul de intersecție al celor 3 mediane ale triunghiului ABCABCABC, și pe verticala prin acest punct se află vârful piramidei SSS.
Relația dintre înălțime și laturile bazei
Dacă:
- latura bazei este aaa,
- înălțimea piramidei este hhh,
- apotema piramidei (înălțimea unei fețe laterale) este lll,
atunci există următoarea relație între aceste elemente:
l2=h2+(a2)2l^2 = h^2 + \left(\frac{a}{2}\right)^2l2=h2+(2a)2
Aceasta derivă din aplicarea teoremei lui Pitagora în triunghiul dreptunghic SOASOASOA, unde:
- SOSOSO este înălțimea piramidei,
- OAOAOA este raza cercului circumscris bazei, adică a3\frac{a}{\sqrt{3}}3a.
Observații importante
Fețele laterale sunt congruente, iar aria lor poate fi calculată ușor odată cunoscute latura bazei și apotema.
Piramida triunghiulară regulată este un caz particular de piramidă regulată, având baza triunghi echilateral și fețele laterale triunghiuri isoscele.
4. Formule specifice
Aria laterală
Aria laterală a unei piramide triunghiulare regulate reprezintă suma ariilor celor trei fețe laterale triunghiulare congruente.
- Fie aaa lungimea laturii bazei și lll apotema piramidei (înălțimea unei fețe laterale).
- Aria unei fețe laterale este:
Afața˘=a⋅l2A_{față} = \frac{a \cdot l}{2}Afața˘=2a⋅l
- Având trei fețe laterale, aria laterală devine:
Alaterala˘=3⋅a⋅l2=3a⋅l2A_{laterală} = 3 \cdot \frac{a \cdot l}{2} = \frac{3a \cdot l}{2}Alaterala˘=3⋅2a⋅l=23a⋅l
Aria totală
Aria totală a piramidei se calculează adunând aria laterală și aria bazei:
Atotala˘=Alaterala˘+Abaza˘A_{totală} = A_{laterală} + A_{bază}Atotala˘=Alaterala˘+Abaza˘
Cum baza este un triunghi echilateral, aria bazei este:
Abaza˘=a234A_{bază} = \frac{a^2\sqrt{3}}{4}Abaza˘=4a23
Astfel:
Atotala˘=3a⋅l2+a234A_{totală} = \frac{3a \cdot l}{2} + \frac{a^2\sqrt{3}}{4}Atotala˘=23a⋅l+4a23
Volumul piramidei
Volumul unei piramide este dat de formula generală:
V=13⋅Abaza˘⋅hV = \frac{1}{3} \cdot A_{bază} \cdot hV=31⋅Abaza˘⋅h
Pentru o piramidă triunghiulară regulată:
V=13⋅a234⋅hV = \frac{1}{3} \cdot \frac{a^2\sqrt{3}}{4} \cdot hV=31⋅4a23⋅h V=a2h312V = \frac{a^2h\sqrt{3}}{12}V=12a2h3
Exemplu practic
Se consideră o piramidă triunghiulară regulată cu:
- latura bazei a=6 cma = 6\,cma=6cm,
- înălțimea piramidei h=8 cmh = 8\,cmh=8cm.
- Determinarea apotemei lll
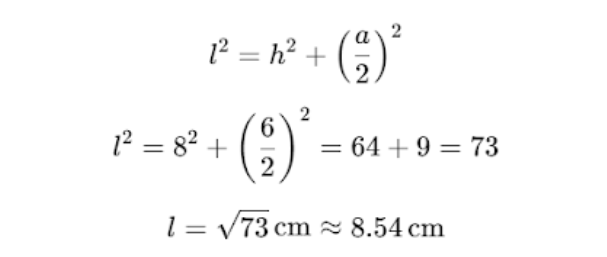
2. Aria laterală

- Aria totală
Abaza˘=a234=6234=3634=93 cm2A_{bază} = \frac{a^2\sqrt{3}}{4} = \frac{6^2\sqrt{3}}{4} = \frac{36\sqrt{3}}{4} = 9\sqrt{3}\,cm^2Abaza˘=4a23=4623=4363=93cm2 Atotala˘=76.86+93≈76.86+15.59≈92.45 cm2A_{totală} = 76.86 + 9\sqrt{3} \approx 76.86 + 15.59 \approx 92.45\,cm^2Atotala˘=76.86+93≈76.86+15.59≈92.45cm2
- Volumul
V=a2h312=62⋅8⋅312V = \frac{a^2h\sqrt{3}}{12} = \frac{6^2 \cdot 8 \cdot \sqrt{3}}{12}V=12a2h3=1262⋅8⋅3 V=36⋅8⋅312=288312=243 cm3V = \frac{36 \cdot 8 \cdot \sqrt{3}}{12} = \frac{288\sqrt{3}}{12} = 24\sqrt{3}\,cm^3V=1236⋅8⋅3=122883=243cm3 V≈41.57 cm3V \approx 41.57\,cm^3V≈41.57cm3
Aplicații în viața reală
- Arhitectură – Piramidele triunghiulare sunt folosite ca elemente decorative sau structurale în construcții moderne datorită stabilității și simetriei lor.
- Design industrial – Structurile cu această formă sunt folosite pentru a distribui uniform greutatea, de exemplu, în suporturi și turnuri metalice.
- Tehnologie și știință – În optică și acustică, piramidele triunghiulare sunt utilizate în dispozitive pentru direcționarea undelor sau a razelor de lumină.
6. Piramida triunghiulară regulată în spațiu
Pentru a analiza piramida triunghiulară regulată în geometria analitică, putem plasa baza și vârful în sistemul de axe OxyzOxyzOxyz:
- Alegem baza triunghiulară echilaterală în planul xyxyxy.
- Vârful piramidei este situat deasupra centrului bazei, pe axa zzz.
O posibilă poziționare:
- A(0,0,0)A(0,0,0)A(0,0,0)
- B(a,0,0)B(a,0,0)B(a,0,0)
- C(a2,a32,0)C\left(\frac{a}{2},\frac{a\sqrt{3}}{2},0\right)C(2a,2a3,0)
- S(a2,a36,h)S\left(\frac{a}{2},\frac{a\sqrt{3}}{6},h\right)S(2a,6a3,h), unde hhh este înălțimea piramidei.
Vectori și plane asociate
- Vectorii muchiilor pot fi exprimați prin coordonatele vârfurilor, de exemplu:
AS→=(a2,a36,h)\overrightarrow{AS} = \left(\frac{a}{2},\frac{a\sqrt{3}}{6},h\right)AS=(2a,6a3,h)
- Ecuația planului unei fețe laterale se determină cu ajutorul a trei puncte necoliniare (S,A,BS, A, BS,A,B).
- Normalele plane sunt utile pentru a calcula unghiurile dintre fețele piramidei.
Exercițiu
Se consideră o piramidă triunghiulară regulată cu latura bazei a=6 cma=6\,cma=6cm și înălțimea h=8 cmh=8\,cmh=8cm, plasată astfel:
- A(0,0,0)A(0,0,0)A(0,0,0),
- B(6,0,0)B(6,0,0)B(6,0,0),
- C(3,33,0)C(3,3\sqrt{3},0)C(3,33,0),
- S(3,3,8)S(3,\sqrt{3},8)S(3,3,8).
Cerinte:
- Determină vectorii muchiilor laterale SA,SB,SCSA, SB, SCSA,SB,SC.
- Calculează lungimea acestor muchii.
Rezolvare
1️⃣ Vectorii muchiilor laterale:
SA→=(3−0,3−0,8−0)=(3,3,8)\overrightarrow{SA} = (3-0,\sqrt{3}-0,8-0) = (3,\sqrt{3},8)SA=(3−0,3−0,8−0)=(3,3,8) SB→=(3−6,3−0,8−0)=(−3,3,8)\overrightarrow{SB} = (3-6,\sqrt{3}-0,8-0) = (-3,\sqrt{3},8)SB=(3−6,3−0,8−0)=(−3,3,8) SC→=(3−3,3−33,8−0)=(0,−23,8)\overrightarrow{SC} = (3-3,\sqrt{3}-3\sqrt{3},8-0) = (0,-2\sqrt{3},8)SC=(3−3,3−33,8−0)=(0,−23,8)
2️⃣ Lungimea muchiei SASASA:
∣SA∣=32+(3)2+82=9+3+64=76≈8.72 cm|SA| = \sqrt{3^2 + (\sqrt{3})^2 + 8^2} = \sqrt{9+3+64} = \sqrt{76} \approx 8.72\,cm∣SA∣=32+(3)2+82=9+3+64=76≈8.72cm
Lungimile celorlalte muchii laterale sunt identice (simetrie).
Importanța analizei tridimensionale
- În modelarea 3D, piramidele triunghiulare sunt utilizate ca elemente de bază în grafică și animații.
- În fizică, analiza coordonatelor este utilă pentru calculul centrelor de greutate și momentelor de inerție.
7. Probleme și exerciții
Exercițiu rezolvat
O piramidă triunghiulară regulată are:
- latura bazei a=8 cma = 8\,cma=8cm,
- înălțimea h=10 cmh = 10\,cmh=10cm.
Un plan secant paralel cu baza intersectează piramida la o distanță de 4 cm4\,cm4cm de vârf. Determină:
- Dimensiunile secțiunii plane formate,
- Aria acestei secțiuni,
- Volumul porțiunii de piramidă situate între această secțiune și baza piramidei.
Rezolvare
1️⃣ Determinarea dimensiunilor secțiunii
Planul secant este paralel cu baza. Deoarece planurile paralele determină secțiuni omotetice, secțiunea formată este un triunghi echilateral, asemenea bazei, cu latura:
a1=a⋅h1ha_1 = a \cdot \frac{h_1}{h}a1=a⋅hh1
unde h1h_1h1 este distanța de la planul secant la baza piramidei:
h1=h−4=10−4=6 cmh_1 = h – 4 = 10 – 4 = 6\,cmh1=h−4=10−4=6cm a1=8⋅610=4.8 cma_1 = 8 \cdot \frac{6}{10} = 4.8\,cma1=8⋅106=4.8cm
2️⃣ Aria secțiunii
Asecțiune=a1234A_{secțiune} = \frac{a_1^2\sqrt{3}}{4}Asecțiune=4a123 Asecțiune=(4.8)234A_{secțiune} = \frac{(4.8)^2\sqrt{3}}{4}Asecțiune=4(4.8)23 Asecțiune=23.0434≈9.983 cm2A_{secțiune} = \frac{23.04\sqrt{3}}{4} \approx 9.98\sqrt{3}\,cm^2Asecțiune=423.043≈9.983cm2 Asecțiune≈17.28 cm2A_{secțiune} \approx 17.28\,cm^2Asecțiune≈17.28cm2
3️⃣ Volumul trunchiului de piramidă
Volumul porțiunii de piramidă între secțiune și baza inițială este diferența dintre volumul piramidei mari și cel al piramidei mici (care are vârful comun și baza secțiunea):
Vmare=a2h312V_{mare} = \frac{a^2h\sqrt{3}}{12}Vmare=12a2h3 Vmare=82⋅10⋅312V_{mare} = \frac{8^2 \cdot 10 \cdot \sqrt{3}}{12}Vmare=1282⋅10⋅3 Vmare=640312≈92.38 cm3V_{mare} = \frac{640\sqrt{3}}{12} \approx 92.38\,cm^3Vmare=126403≈92.38cm3 Vmic=a12h1312V_{mic} = \frac{a_1^2h_1\sqrt{3}}{12}Vmic=12a12h13 Vmic=(4.8)2⋅6⋅312V_{mic} = \frac{(4.8)^2 \cdot 6 \cdot \sqrt{3}}{12}Vmic=12(4.8)2⋅6⋅3 Vmic≈19.48 cm3V_{mic} \approx 19.48\,cm^3Vmic≈19.48cm3 Vtrunchi=Vmare−Vmic≈92.38−19.48=72.9 cm3V_{trunchi} = V_{mare} – V_{mic} \approx 92.38 – 19.48 = 72.9\,cm^3Vtrunchi=Vmare−Vmic≈92.38−19.48=72.9cm3
Probleme propuse pentru aprofundare
1. Determină aria laterală, aria totală și volumul unei piramide triunghiulare regulate cu a=7 cma = 7\,cma=7cm, h=9 cmh = 9\,cmh=9cm.
2. O piramidă triunghiulară regulată are aria totală de 150 cm2150\,cm^2150cm2 și înălțimea h=8 cmh=8\,cmh=8cm. Află lungimea laturii bazei.
3. Printr-o piramidă triunghiulară regulată trece un plan paralel cu baza și situat la o distanță de 3 cm3\,cm3cm de vârf. Determină volumul trunchiului de piramidă astfel format, dacă a=9 cma=9\,cma=9cm și h=12 cmh=12\,cmh=12cm.
4. Într-un sistem de coordonate, consideră o piramidă triunghiulară regulată cu:
A(0,0,0),B(6,0,0),C(3,33,0),S(3,3,8)A(0,0,0), B(6,0,0), C(3,3\sqrt{3},0), S(3,\sqrt{3},8)A(0,0,0),B(6,0,0),C(3,33,0),S(3,3,8).
Determină ecuația planului feței SBCSBCSBC.
5. Un obiect cu forma unei piramide triunghiulare regulate este acoperit cu un strat de vopsea de 0.3 mm0.3\,mm0.3mm. Determină volumul stratului de vopsea dacă a=5 cma=5\,cma=5cm, h=10 cmh=10\,cmh=10cm.
Piramida triunghiulară regulată este un corp geometric fundamental, caracterizat printr-o bază triunghi echilateral și fețe laterale triunghiuri isoscele congruente. În cadrul acestui articol am definit elementele sale principale – muchii, vârfuri, fețe – și am explorat proprietățile geometrice care îi conferă simetrie și eleganță. Am dedus formulele pentru aria laterală, aria totală și volum și am ilustrat aplicabilitatea acestora prin exemple și exerciții practice.
Relevanța piramidei triunghiulare regulate în geometria spațială
Studiul acestui corp geometric oferă o bază solidă pentru înțelegerea formelor tridimensionale mai complexe. În arhitectură și design, piramida triunghiulară este apreciată pentru stabilitatea structurală și estetica sa. În matematică, ea servește drept model pentru explorarea secțiunilor plane, a vectorilor în spațiu și a simetriilor.
Perspective și aplicații
Analiza piramidei triunghiulare regulate deschide calea către subiecte avansate precum prisma și piramidele cu baze poligonale cu mai multe laturi, corpurile de rotație și poliedrele regulate. De asemenea, conceptele învățate aici pot fi aplicate în domenii variate, de la inginerie la grafică computerizată.

Leave a Reply