Teorema bisectoarei este o proprietate geometrică fundamentală care leagă unghiurile și laturile unui triunghi și afirmă că bisectoarea unui unghi al unui triunghi împarte latura opusă în segmente proporționale cu celelalte două laturi ale triunghiului. Cu alte cuvinte, dacă un unghi al triunghiului este împărțit în două unghiuri egale de o bisectoare, atunci punctul de intersecție de pe latura opusă împarte acea latură în două segmente a căror lungimi sunt direct proporționale cu lungimile celorlalte două laturi ale triunghiului. Această teoremă este folosită în demonstrațiile geometrice și în rezolvarea unor probleme care implică proporții și rapoarte în triunghiuri.
Ce este o bisectoare
Conform CueMath, o bisectoare este o semidreaptă care împarte un unghi în două unghiuri congruente (egale). În cazul unui triunghi, fiecare unghi interior are propria sa bisectoare, care pornește din vârful unghiului și ajunge pe latura opusă, formând două unghiuri egale la vârf.
Caracteristici ale bisectoarei unui unghi:
- Împarte unghiul în două părți egale
- Este unică pentru fiecare unghi
- Într-un triunghi, cele trei bisectoare interioare se întâlnesc într-un punct numit centrul cercului înscris, adică punctul din care se poate trasa un cerc care atinge toate cele trei laturi ale triunghiului (cercul înscris)
Bisectoarea nu trebuie confundată cu mediatoarea sau cu înălțimea, care sunt alte linii importante în geometrie.
Proprietăți matematice ale bisectoarei
- Bisectoarea unui unghi dintr-un triunghi împarte acel unghi în două părți egale.
- Împarte latura opusă în segmente proporționale cu laturile adiacente
- Toate cele trei bisectoare interioare se intersectează într-un punct comun care este centrul cercului înscris în triunghi (cercul care atinge toate cele trei laturi ale triunghiului).
- Bisectoarea nu este neapărat perpendiculară pe latura opusă și nu trebuie confundată cu înălțimea triunghiului, care este perpendiculară pe latura opusă vârfului.
Aceste proprietăți sunt utile atât în demonstrații teoretice, cât și în rezolvarea problemelor geometrice practice.
Teorema bisectoarei
Teorema bisectoarei este una dintre cele mai importante relații din geometria triunghiului, fiind importantă în studiul proporțiilor și al construcțiilor geometrice. Aceasta oferă o legătură între unghiurile triunghiului și lungimile laturilor sale.
Definirea teoremei bisectoarei
Enunțul teoremei:
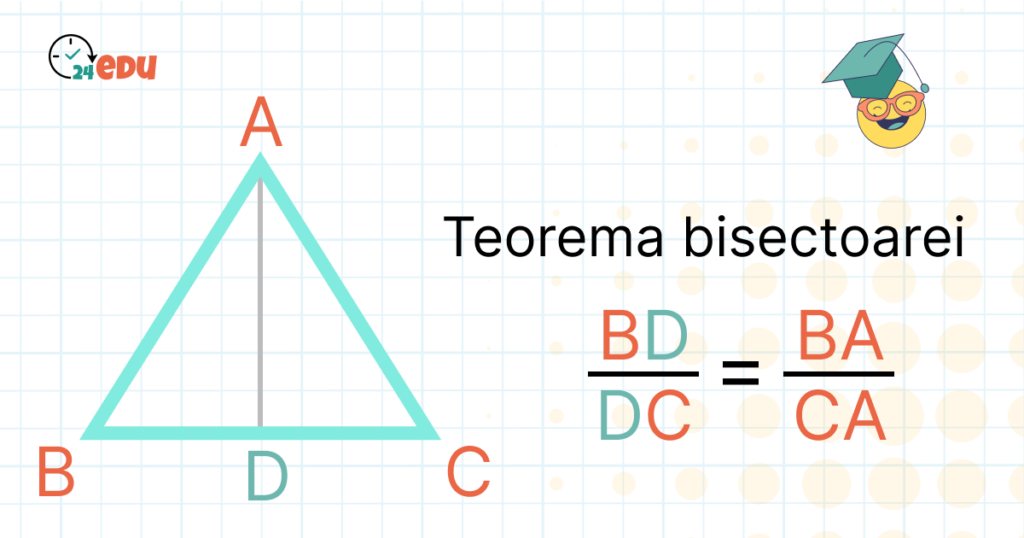
Fie triunghiul 𝐴𝐵𝐶 și fie 𝐴𝐷 bisectoarea unghiului:
Cu alte cuvinte, bisectoarea unui unghi dintr-un triunghi împarte latura opusă în două segmente proporționale cu lungimile laturilor adiacente acelui unghi.
Elementele implicate în teoremă
Triunghiul 𝐴𝐵𝐶
ABC – triunghi oarecare (nu se impun condiții speciale precum dreptunghi)
Teorema bisectoarei afirmă că, într-un triunghi, bisectoarea unui unghi împarte latura opusă în două segmente proporționale cu laturile adiacente acelui unghi. Cu alte cuvinte, dacă luăm un triunghi oarecare și trasăm bisectoarea unui unghi interior, punctul în care aceasta intersectează latura opusă împarte acea latură în două părți care respectă proporția determinată de lungimile celorlalte două laturi ale triunghiului.
Bisectoarea este o semidreaptă care pornește dintr-un vârf al triunghiului și împarte unghiul respectiv în două unghiuri egale. Aceasta nu este, în general, perpendiculară pe latura opusă și nici nu împarte latura în mod egal, ci în funcție de lungimile celorlalte două laturi.
Teorema bisectoarei are aplicații importante în demonstrațiile geometrice, în construcții cu rigla și compasul, precum și în probleme de geometrie analitică sau trigonometrică. Ea este valabilă pentru orice tip de triunghi – acutunghic, obtuzunghic sau dreptunghic – și poate fi extinsă și la bisectoarele exterioare, cu anumite adaptări.
În plus, bisectoarele celor trei unghiuri ale unui triunghi se intersectează într-un punct unic numit incentru, care este centrul cercului înscris în triunghi, adică acel cerc care este tangent la toate cele trei laturi.
Cine a descoperit teorema bisectoarei?
Originea teoremei bisectoarei este strâns legată de dezvoltarea geometriei în Antichitate, în special de lucrările matematicienilor greci. Deși nu există o persoană anume căreia să-i fie atribuită în mod clar „descoperirea” acestei teoreme, ea este cel mai adesea asociată cu Euclid, unul dintre cei mai influenți matematicieni ai lumii antice.
Euclid a trăit în jurul anului 300 î.Hr., în Alexandria (Egiptul elenistic), și este cunoscut mai ales pentru lucrarea sa monumentală, „Elementele”, un tratat în 13 volume care a sistematizat cunoștințele geometrice ale vremii. Deși în Elementele nu regăsim teorema bisectoarei exprimată exact în forma cunoscută azi, ideea de proporționalitate între laturile unui triunghi și segmentele determinate de o bisectoare este prezentă în mod implicit, sub formă de propoziții geometrice și raționamente logice.
În acea perioadă, geometria era tratată fără formule sau notații algebrice, totul fiind exprimat prin construcții și demonstrații pur vizuale, bazate pe riglă și compas. Teorema bisectoarei, așa cum o cunoaștem azi, a fost formulată mai târziu în termeni moderni, când matematica a început să combine geometria cu algebra, în special începând cu perioada Renașterii.
În secolele al XVII-lea și XVIII-lea, odată cu apariția geometriei analitice (prin Descartes și alți gânditori), proprietăți precum teorema bisectoarei au fost reformulate într-un limbaj algebric, cu raporturi, fracții și ecuații. Acest pas a făcut posibilă aplicarea teoremei într-un mod mult mai general și abstract.
Așadar:
- Euclid este considerat sursa timpurie a ideii din spatele teoremei bisectoarei, deși nu a enunțat-o în forma actuală.
- Forma modernă a teoremei este rezultatul unei evoluții de peste 2000 de ani, în care geometria s-a îmbinat cu algebra.
- Importanța teoremei a crescut odată cu dezvoltarea matematicii moderne, devenind o unealtă de bază în studiul triunghiurilor, proporțiilor și aplicațiilor geometrice.
- Teorema bisectoarei nu este creația unui singur matematician, ci rezultatul unei construcții colective, rafinate de-a lungul istoriei matematicii.
Bisectoarea triunghiului ca lecție despre armonie
Triunghiul este una dintre cele mai vechi și fundamentale forme geometrice studiate de omenire. Fiind cea mai simplă figură plană definită de trei puncte necoliniare, triunghiul stă la baza geometriei plane și este prezent atât în construcțiile abstracte ale matematicii, cât și în lumea concretă – de la arhitectură și inginerie până la artă și natură. În ciuda simplității sale aparente, triunghiul ascunde o complexitate fascinantă, iar una dintre cele mai elegante structuri interne ale sale este bisectoarea.
Bisectoarea este o semidreaptă care pleacă dintr-un vârf al triunghiului și împarte unghiul în două părți egale. Această împărțire simetrică a unghiului aduce cu sine o proprietate remarcabilă: punctul în care bisectoarea întâlnește latura opusă împarte acea latură în două segmente proporționale cu celelalte două laturi ale triunghiului. Astfel, bisectoarea nu doar creează echilibru în interiorul triunghiului, ci și stabilește o relație armonioasă între unghiuri și laturi, oferind o punte între formă și măsură.
În plus, cele trei bisectoare ale unghiurilor unui triunghi se întâlnesc într-un punct unic numit incentru, care este centrul cercului înscris. Acesta este singurul cerc care atinge toate cele trei laturi ale triunghiului, iar construcția sa este posibilă tocmai datorită proprietăților bisectoarelor. Această idee de simetrie perfectă și întâlnire într-un punct comun reflectă ordinea internă a triunghiului și frumusețea structurii sale.
Importanța bisectoarelor nu se limitează la teorie. Ele sunt utilizate în construcții geometrice, în proiectarea de spații echilibrate în arhitectură, în algoritmi informatici pentru procesarea formelor, dar și în rezolvarea problemelor complexe din matematică. În toate aceste contexte, bisectoarele devin un simbol al echilibrului și al relației exacte dintre părțile unui întreg.
Așadar, triunghiul, în simplitatea sa, ascunde structuri de o mare subtilitate, iar bisectoarele sunt printre cele mai rafinate elemente ale sale. Ele îmbină estetica cu logica, simetria cu funcționalitatea, demonstrând că în spatele unor forme elementare se pot afla idei profunde și aplicații vaste. Prin studierea lor, nu învățăm doar despre geometrie, ci și despre armonia ascunsă în formele lumii.
La ce este utilizată teorema bisectoarei?
Teorema bisectoarei este folosită în numeroase contexte din geometrie și are aplicații practice și teoretice importante.
Determinarea proporțiilor într-un triunghi
Teorema bisectoarei este importantă când vrem să aflăm cât măsoară un segment de pe una dintre laturile triunghiului, atunci când știm lungimile celorlalte laturi și poziția bisectoarei.
Rezolvarea problemelor geometrice
Este folosită frecvent în probleme de tip olimpic sau în exerciții de geometrie clasică, unde se cere determinarea unor lungimi necunoscute sau demonstrarea unor relații între segmente.
Construcții geometrice
Teorema este utilă în construcții cu rigla și compasul, în special atunci când trebuie să se traseze o linie care împarte o latură în segmente proporționale sau când se construiește cercul înscris într-un triunghi.
Determinarea centrului cercului înscris
Cele trei bisectoare ale unghiurilor unui triunghi se întâlnesc într-un punct numit incentru, care este centrul cercului înscris. Cunoașterea bisectoarelor permite trasarea exactă a acestui cerc.
Aplicații în geometria analitică
În geometria cu coordonate, teorema bisectoarei poate fi utilizată pentru a determina poziția unui punct care împarte un segment în proporție cu două distanțe cunoscute, oferind o punte între geometria sintetică și algebraică.
Proiecte de arhitectură și design
În desenul tehnic sau arhitectură, unde este nevoie de proporții precise în împărțirea unor spații sau unghiuri, teorema bisectoarei poate fi aplicată pentru a menține echilibrul și simetria.
Teorema bisectoarei este, așadar, mult mai mult decât o simplă relație teoretică – este un instrument matematic cu aplicații reale, important în înțelegerea și manipularea formelor geometrice.
Ce alte linii sunt importante în triunghi?
Într-un triunghi, pe lângă bisectoare, mai există și alte linii importante, fiecare având un rol geometric specific și proprii puncte notabile:
Mediatoarea unei laturi – Este o dreaptă perpendiculară pe mijlocul unei laturi. Punctul unde se intersectează cele trei mediatoare ale laturilor este numit circumcentru, centrul cercului circumscris triunghiului.
Mediană – Este segmentul care unește un vârf al triunghiului cu mijlocul laturii opuse. Cele trei mediane se intersectează într-un punct numit centru de greutate sau baricentru, care este punctul de echilibru al triunghiului.
Înălțime – Este segmentul perpendicular dus dintr-un vârf pe latura opusă (sau pe prelungirea acesteia). Înălțimile se întâlnesc într-un punct numit ortocentru.
Bisectoare exterioare. Sunt bisectoarele unghiurilor formate între o latură și prelungirea altei laturi. Acestea sunt folosite pentru a construi cercurile exînscrise ale triunghiului.
Transversala lui Menelaus. Este o dreaptă care taie cele trei laturi ale triunghiului (sau prelungirile acestora) în puncte coliniare. Este importantă în demonstrații și teoreme legate de coliniaritate și proporții.
Transversala lui Ceva. Este o dreaptă care unește un vârf al triunghiului cu un punct de pe latura opusă. Cele trei astfel de drepte concurente (una din fiecare vârf) se întâlnesc într-un punct comun dacă se respectă anumite condiții de proporționalitate (Teorema lui Ceva).
Fiecare dintre aceste linii are un rol precis și se intersectează în puncte remarcabile ale triunghiului, care contribuie la înțelegerea profundă a structurii sale geometrice. Ele sunt importante atât în geometria clasică, cât și în aplicații moderne.
În ce domenii se folosește teorema bisectoarei?
Teorema bisectoarei are aplicații în mai multe domenii, nu doar în matematică teoretică. Chiar dacă este o relație geometrică simplă, ea apare în contexte variate, de la educație până la arhitectură sau informatică.
Matematică și educație
Este un concept de bază predat în școală, fiind folosit în probleme, demonstrații, construcții geometrice și olimpiade. Ajută elevii să înțeleagă proporțiile, simetria și proprietățile triunghiurilor.
Geometrie computațională
În informatică, teorema bisectoarei este utilizată în algoritmi care implică triunghiuri, cum ar fi triangularea poligoanelor, grafuri geometrice sau generarea de rețele (mesh-uri) în grafică 3D.
Arhitectură și design
Este folosită în construcția de forme echilibrate și proporționale. Arhitecții o aplică în proiectarea structurilor simetrice, în desen tehnic și în împărțirea spațiilor interioare sau exterioare.
Inginerie
Este aplicată în modelarea structurilor mecanice sau construcțiilor. Poate apărea în calculul tensiunilor, proiectarea elementelor de susținere și în simulări geometrice.
Topografie și cartografie
Se folosește în împărțirea unor suprafețe în mod proporțional și în determinarea unor puncte precise pe hărți sau terenuri, mai ales când se lucrează cu unghiuri și distanțe.
Artă și design grafic
Principiile proporției și echilibrului vizual se bazează adesea pe concepte geometrice. Teorema bisectoarei ajută la trasarea unor compoziții armonioase și echilibrate în pictură, sculptură sau design digital.
Robotica și navigația autonomă
Algoritmi de luare a deciziilor spațiale pot folosi concepte de împărțire a spațiului și proporții, unde ideile din spatele teoremei bisectoarei sunt aplicate indirect.
Chiar dacă în unele dintre aceste domenii nu se folosește teorema explicit, principiile geometrice din spatele ei apar în mod natural în calcule, construcții sau modelări.
Bisectoarea este o linie fundamentală în geometria triunghiului, având un rol important în înțelegerea relațiilor dintre unghiuri și laturi. Prin proprietățile sale, ea leagă noțiunea de simetrie cu ideea de proporționalitate și contribuie la construirea unor puncte remarcabile precum centrul cercului înscris. Utilizată atât în matematică teoretică, cât și în aplicații practice precum arhitectura, ingineria sau informatica, bisectoarea rămâne un instrument geometric de bază, cu valoare educativă și aplicativă durabilă.

Leave a Reply