Teorema catetei

În geometria triunghiului dreptunghic, teorema catetei este una dintre cele mai utile relații, iar în cele ce urmează, ne propunem să îți vorbim mai mult despre ea, pentru a o înțelege mai ușor.

Ce este teorema catetei

Teorema catetei este o relație geometrică ce ajută la calcularea lungimilor necunoscute dintr-un triunghi dreptunghic, dar și la probleme de geometrie și spațiu. Ea le este predată elevilor de gimnaziu și este de obicei înțeleasă destul de ușor, dacă ești atent și exersezi.

Teorema catetei este o teoremă conform căreia într-un triunghi dreptunghic, lungimea unei catete este formată din media geometrică dintre lungimea proiecției sale pe ipotenuză și lungimea ipotenuzei.

Dacă nu ai cunoștințe prea multe în domeniul matematicii, totul ar putea părea dificil, dar, să le luăm pe rând. Vrem ca în cele ce urmează să îți explicăm puțin fiecare termen în parte:

cateta

Un triunghi dreptunghic are o latură mai lungă și două mai scurte. Ei bine, cateta este una dintre laturile scurte ale unui triunghi dreptunghic.

triunghi dreptunghic

Triunghiul dreptunghic este acel triunghi care are un unghi de 90°. El reprezintă o figură geometrică foarte importantă, având proprietăți speciale.

media geometrică

Media geometrică este o valoare care indică o tendință centrală sau o valoare tipică a unui set de numere sau termeni. Se calculează prin formula: mg = a ⋅ b.

lungimea proiecției

Lungimea proiecției face referire la „umbra” pe care o lasă cateta pe ipotenuză, dacă se coboară perpendicular din vârful ipotenuzei. Aceasta reprezintă o distanță și este întotdeauna mai mică sau egală cu cateta.

ipotenuză

Ipotenuza este cea mai lungă latură dintr-un triunghi dreptunghic și este acea latură care se opune unghiului drept.

Cum se enunță teorema catetei și ce formulă are

Teorema catetei, așa cum am amintit și mai sus, se enunță astfel: într-un triunghi dreptunghic, pătratul lungimii unei catete este egal cu produsul dintre lungimea ipotenuzei și lungimea proiecției pe ipotenuză a respectivei catete.

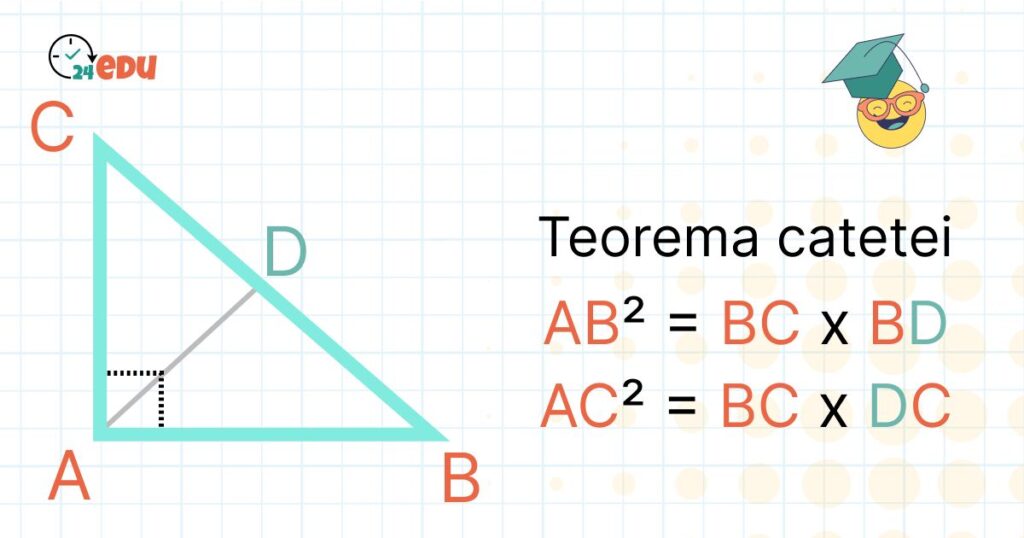
Mai exact, se dă un triunghi dreptunghic ABC, cu unghiul A fiind unghi drept.

În acest triunghi:

AB și AC sunt catetele;
BC este ipotenuza;
AD este înălțimea din A pe ipotenuză;
BD este proiecția catetei AB;
DC este proiecția catetei AC.

Acestea fiind zise, avem următoarele:

AB² = BC ⋅ BD
AC² = BC ⋅ DC

Prin urmare, fiecare catetă este media geometrică dintre ipotenuză și proiecția ei pe ipotenuză.

De unde vine această teoremă

În ceea ce privește originea acestei teoreme, nu există un nume clar legat de această descoperire. Euclid însă, în cartea sa Elementele, o amintește într-o formă geometrică, prin construcții și comparații de arii.

De fapt, această teoremă este considerată a fi o consecință a teoremei înălțimii, având strânsă legătură cu teorema lui Pitagora.

Demonstrația teoremei catetei

Pentru a demonstra această teoremă, se dă AD 丄 BC, unde D ∊ BC, BD este proiecția catetei AB, DC este proiecția catetei AC. Acestea fiind zise, avem două triunghiuri asemănătoare, și anume ∆ ABD și ∆ CBA. Din aceste informații rezultă proporția:

Din această proporție putem trage concluzia că AB² = BC ⋅ BD, așadar AB = DB ⋅ BC.

Diferența dintre teorema catetei și teorema lui Pitagora

Chiar dacă se aplică doar triunghiurilor dreptunghice, teorema catetei nu este la fel cu cea a lui Pitagora, iar diferențele apar în ce exprimă fiecare relație în parte.

Teorema lui Pitagora

Această teoremă spune că într-un triunghi dreptunghic, pătratul lungimii ipotenuzei este egal cu suma pătratelor lungimilor catetelor, în conformitate cu formula: c² = a² + b², unde c este ipotenuza și a și b sunt catetele.

Această teoremă leagă laturile triunghiului dreptunghic și se folosește pentru a calcula lungimea unei laturi atunci când se cunoaște lungimea celorlalte două.

Această teoremă spune că într-un triunghi dreptunghic, , pătratul unei catete este egal cu produsul dintre lungimea ipotenuzei și lungimea proiecției acelei catete pe ipotenuză, în conformitate cu formulele: AB² = BC ⋅ BD și AC² = BC ⋅ DC, unde AB și AC sunt catetele, BC este ipotenuza și BD și DC sunt proiecțiile catetelor pe ipotenuză.

Această teoremă leagă o catetă, ipotenuza și proiecția catetei pe ipotenuză și o folosim atunci când știm o catetă și vrem să o aflăm pe cealaltă.

Când folosim teorema catetei în matematică

Teorema catetei poate fi utilizată în mai multe situații, iar pe unele dintre cele mai comune ți le vom prezenta acum.

când cunoaștem ipotenuza și proiecția unei catete

În primul rând, această teoremă este folosită pentru a calcula o catetă a cărei valoare nu o cunoaștem. Însă, pentru asta este necesar să avem câteva date și anume: lungimea ipotenuzei și cea a proiecției catetei pe ipotenuză.

când avem o înălțime care coboară dintr-un unghi drept

Teorema catetei poate fi folosită și atunci când avem o înălțime care coboară dintr-un unghi drept pe ipotenuză și o împarte în două. Astfel, se pot afla catetele și segmentele de pe ipotenuză și se pot face tot felul de probleme geometrice.

când nu se poate folosi teorema lui Pitagora

Dacă nu avem datele necesare pentru a folosi teorema lui Pitagora, de cele mai multe ori se poate folosi teorema catetelor. Bineînțeles, acest lucru se poate face doar dacă sunt disponibile datele enunțate mai sus.

când avem probleme de geometrie sintetică

Dacă este necesar să afli lungimi fără a folosi radicali sau trigonometrie, teorema catetei poate fi de ajutor. Ea permite demonstrații, egalități sau raporturi între segmente, dacă este vorba de un triunghi dreptunghic.

Greșeli frecvente și cum să le eviți

Când elevii sau chiar adulții care au nevoie de diverse calcule lucrează cu teorema catetei, sunt anumite greșeli care pot să apară. Vrem să îți vorbim puțin despre ele, în cele ce urmează, pentru a ști la ce să fii atent.

folosirea teoremei lui Pitagora în loc de teorema catetei

Când lucrezi cu teorema catetei, ai în vedere clar formula ei, și aplic-o în mod corect. Nu ai a² + b² = c² (ipotenuza la pătrat este egală cu suma pătratelor lungimilor catetei), cum se întâmplă în cazul teoremei lui Pitagora, ci ai cateta ² = ipotenuza x proiecția.

Așadar, teorema catetei lucrează cu proiecția. Îți vei da seama de asta din enunțul problemei, unde se va menționa o înălțime care coboară pe ipotenuză sau segmentele BD, DC.

folosirea greșită a proiecției

Ai grijă să folosești proiecțiile corecte pentru fiecare catetă. Pentru cateta AB, proiecția corectă este BD, nu DC. Poți să eviți greșelile desenând un triunghi și marcând corect și clar segmentele.

Ai permanent în minte faptul că proiecția unei catete este paralelă cu acea catetă pe ipotenuză.

aplicarea teoremei catetei în triunghiuri care nu sunt dreptunghice

Nu uita că această teoremă se aplică doar la triunghiuri dreptunghice, adică la acele triunghiuri care au un unghi de 90°.

neînțelegerea termenului de proiecție

Proiecția poate părea dificilă într-o primă fază, dar nu este de fapt nimic foarte complicat. Proiecția este acel segment de pe ipotenuză (latura care se opune unghiului drept) care se află direct sub catetă, dar nu este toata ipotenuza.

Pentru a obține clar proiecția, trebuie să trasezi din unghiul drept o linie din perpendiculară, care o să cadă pe ipotenuză. Proiecția va fi segmentul de la intersecția liniei perpendiculare cu ipotenuza, până în unghiul care se află în capătul catetei respective.

Sfaturi pentru a învăța ușor această teoremă

Dacă ești elev și trebuie să înveți teorema catetei, este posibil ca la început să te simți puțin copleșit. Pentru a fi totul cât mai simplu, avem pentru tine câteva sfaturi:

ai mereu în față un desen care să te ajute să vizualizezi cu ușurință triunghiu, unghiul drept, perpendiculara care cade din unghiul drept, proiecția etc. Astfel va fi totul mult mai ușor de înțeles.
încearcă să înveți totul logic, nu mecanic, deoarece acest lucru te va ajuta mult mai ușor și când va trebui să aplici formula în exerciții sau în practică.
rezolvă exercițiile în mod gradual. Începe cu unele simple, iar după ce le-ai deslușit și le-ai înțeles, crește nivelul de dificultate.
găsește în jurul tău tot felul de obiecte care te pot ajuta să faci analogii și să înțelegi mai bine ce trebuie să faci. Te poți folosi, de exemplu, de o rampă.
asigură-te că înțelegi foarte bine toți termenii folosiți în teorema catetei, termeni pe care i-am explicat și noi la început.
fii atent la unitățile de măsură folosite, dar și la semnele de punctuație, deoarece orice mică greșeală poate da peste cap toate calculele.

Curiozități matematice legate de triunghiurile dreptunghice

Matematica este un domeniu fascinant și plin de informații interesante, informații pe care e bine să le cunoști pentru a-ți dezvolta cultura generală. Acum, vrem să discutăm puțin despre câteva curiozități interesante legate de triunghiurile dreptunghice.

conform Math is Fun, triunghiul dreptunghic a fost inspirație pentru una dintre cele mai mari teoreme matematice din lume și anume Teorema lui Pitagora. Această teoremă era însă cunoscută și aplicată chiar cu mulți ani înainte, de către civilizațiile babiloniene și egiptene.
indiferent de unitatea de măsură pe care o folosești pentru lungimea laturilor unui triunghi, dacă acestea sunt de 3, 4 și 5 m/cm/ha etc., în mod garantat vorbim de un triunghi dreptunghic.
dacă vei coborî din unghiul drept al unui triunghi o dreaptă perpendiculară pe ipotenuză, vei forma două triunghiuri mai mici, asemănătoare cu triunghiul mare. Această dreaptă perpendiculară este foarte importantă, deoarece din ea derivă nu doar teorema catetei, ci și cea a înălțimii, cum ne spune și Wikipedia.
dacă ai un triunghi dreptunghic cu un unghi de 90° și altul de 30°, întotdeauna cateta opusă unghiului de 30° va fi jumătate din ipotenuză, iar raportul dintre laturi va fi unul egal.
triunghiurile dreptunghice sunt extrem de importante când vorbim de trigonometrie, deoarece orice diagonală pe care o tratăm într-un cub sau o prismă va forma în spațiu un triunghi dreptunghic.
doar cu ajutorul unei sfori poți construi cu ușurință un triunghi dreptunghic, ceea ce făceau și egiptenii când construiau pentru a obține colțuri drepte. Aceștia foloseau o sfoară cu 12 noduri și cu ajutorul ei formau unghiuri drepte.
marele matematician și artist Leonardo da Vinci s-a folosit foarte mult de triunghiul dreptunghic în studiile sale despre proporții, construcții sau perspective. Aceste triunghiuri pot fi observate frecvent și în arhitectura gotică.
triunghiurile dreptunghice pot fi folosite pentru a realiza pătrate perfecte sau figuri mai complexe. De exemplu, dacă iei două triunghiuri dreptunghice identice și le lipești ipotenuzele, vei obține un pătrat perfect. Totodată, triunghiurile dreptunghice sunt folosite și în puzzle precum Tangram.

Nu-i așa că ți-am stârnit interesul cu privire la cât de fascinante pot fi aceste forme geometrice? Matematica este într-adevăr un domeniu fascinant, care merită explorat.

Test fulger – verifică ce ai învățat

Ce ai zice să testăm puțin cunoștințele pe care le-ai acumulat citind acest text? Hai să începem:

1. Într-un triunghi dreptunghic, cateta este:

a) mai lungă decât ipotenuza

b) latura opusă unghiului drept

c) una dintre laturile care formează unghiul drept

2. Completează:

Teorema catetei: ___² = ____ x ____

3. Proiecția unei catete se află:

a) pe înălțime

b) pe cateta opusă

c) pe ipotenuză

4. Adevărat sau Fals: Teorema catetei poate fi aplicată în orice triunghi, indiferent de unghiuri.

5. Dacă într-un triunghi dreptunghic avem: ipotenuza = 10 cm, proiecția unei catete = 4 cm
atunci cateta este:

a) 6 cm

b) √40 cm

c) 14 cm

6. Câte triunghiuri se formează atunci când cobori înălțimea din unghiul drept pe ipotenuză?

7. Adevărat sau Fals: Toate triunghiurile pitagoreice au cel puțin o catetă egală cu 5.

8. Într-un triunghi dreptunghic, pătratul unei catete este egal cu:

a) produsul ipotenuzei și proiecției

b) suma catetelor

c) dublul proiecției

9. Teorema catetei derivă din:

a) asemănarea triunghiurilor

b) teorema lui Thales

c) un calcul aproximativ

10. Care dintre formule este corectă?

a) AB² = BD · AC

b) AB² = BC · BD

c) AB² = AD · BD

Răspunsuri:

1. c) una dintre laturile care formează unghiul drept

Catetele sunt cele două laturi care formează unghiul drept într-un triunghi dreptunghic.

2. Catetă² = ipotenuză × proiecție

Aceasta este formula de bază a teoremei catetei.

3. c) pe ipotenuză

Proiecția catetei este un segment de pe ipotenuză.

4. Fals

Teorema catetei se aplică doar în triunghiurile dreptunghice.

5. b) √40 cm

Cateta² = 10 × 4 = 40 ⇒ Cateta = √40 cm

6. 3 triunghiuri

Cele două triunghiuri mai mici (ABD și ADC) + triunghiul mare (ABC)

7. Fals

De exemplu, triunghiul pitagoreic 7-24-25 nu are nicio catetă egală cu 5.

8. a) produsul ipotenuzei și proiecției

Asta e chiar definiția teoremei catetei.

9. a) asemănarea triunghiurilor

Teorema catetei se demonstrează folosind triunghiurile asemănătoare formate de înălțimea pe ipotenuză.

10. b) AB² = BC · BD

AB este cateta, BC este ipotenuza, iar BD este proiecția catetei AB pe ipotenuză.

Dacă ai ajuns până aici, înseamnă că deja știi mai multe despre teorema catetei, acest instrument esențial în problemele de geometrie. Succes în a aplica în practică tot ceea ce ai învățat și astăzi!

Teorema catetei – Formula și definiție