Teorema cosinusului

Matematica este o știință exactă care cuprinde o mulțime de teoreme foarte interesante care astăzi ne fac viața mult mai ușoară. Printre acestea se numără și teorema cosinusului, care este o generalizare a teoremei lui Pitagora.

Dar, înainte de a trece la exemplificări și exemple concrete, să vedem care este legătura dintre geometria triunghiurilor și viața reală, dar și cine a descoperit această teoremă.

Ce legătură are geometria triunghiurilor cu viața reală

Chiar dacă de multe ori nu ne dăm seama, geometria triunghiurilor este de o mare importanță în viața reală. În acest sens, îți prezentăm acum o serie de exemple care te vor face să îți dai seama cât de importantă e mai ales când vorbim de precizie:

navigație și GPS – cu toții folosim aplicațiile care ne ajută să ajungem în diverse locuri. În spatele acestora sta triangulația, care poate stabili cu ajutorul triunghiurilor unde ne aflăm pe o hartă. Triangulația este utilizată inclusiv pe cale aeriană sau navală.
inginerie și proiectare – cu ajutorul triunghiurilor, inginerii calculează forțele și mișcările în proiectarea de mașini, avioane și roboți. Totodată, inginerii se folosesc de geometria triunghiurilor și pentru a analiza structurile metalice, astfel încât să poată prezice cum anume se vor comporta anumite piese aflate în mișcare.
construcții și arhitectură – inginerii constructori și arhitecții se folosesc de triunghiuri pentru a oferi stabilitate în realizarea de poduri, acoperișuri sau structuri metalice, dar și pentru a calcula cu precizie lungimi, înălțimi și unghiuri care nu pot fi măsurate în mod direct.
artă și design – chiar dacă ar putea părea banal, în fotografie, pictură sau design, triunghiurile sunt utilizate pentru a crea proporții cât mai bine echilibrate vizual.
cartografie și topografie – specialiștii din aceste domenii se folosesc de teorema cosinusului pentru a calcula distanțe care nu pot fi măsurate în mod direct.

Data viitoare, când ai tendința de a spune că geometria triunghiurilor nu este ceva foarte important sau nu e aplicabilă în viața de zi cu zi, gândește-te la toate aceste exemple. O parte dintre ele sunt foarte bine exemplificate de către cei de la Math is Fun.

Cine a descoperit teorema cosinusului și cum s-a dezvoltat ea

În privința acestei teorii nu există un autor clar, așa cum aflăm și de pe Wikipedia. Ea a fost descoperită de-a lungul timpului, prin contribuția mai multor oameni de știință, matematicieni, filozofi, interesați de geometrie și trigonometrie.

Această teoremă mai poartă și numele de teorema lui Pitagora generalizată și a ajutat la demonstrarea altor teoreme precum cea a lui Stewart sau a paralelogramului.

Primele dovezi scrise cu privire la această teoremă au apărut prin anii 300 î.Hr., în Elementele, Cartea a II-a, a lui Euclid. Acolo însă nu se spune explicit despre teorema cosinusului, pentru că la acea vreme nu existau termeni precum trigonometrie, dar ideea era exprimată în termeni algebrici.

Teorema cosinusului a fost lansată în forma sa modernă prin secolele XV-XVI, conform celor spuse de Glen Van Brummelen, în cartea The Mathematics of the Heavens and the Earth: The Early History of Trigonometry. Se pare că Johannes Müller și François Viète au fost cei care au formalizat relațiile trigonometrice.

Teorema cosinusului, așa cum o știm astăzi, a apărut în secolele XVII-XVIII, când s-a dezvoltat analiza matematică.

Teorema cosinusului – definiție și formulă

Conform definiției, teorema cosinusului este o teoremă care afirmă faptul că într-un triunghi oarecare, pătratul lungimii unei laturi este egal cu suma pătratelor lungimilor celorlalte două laturi, minus produsul acestora și cosinusul unghiurilor cuprinse între ele.

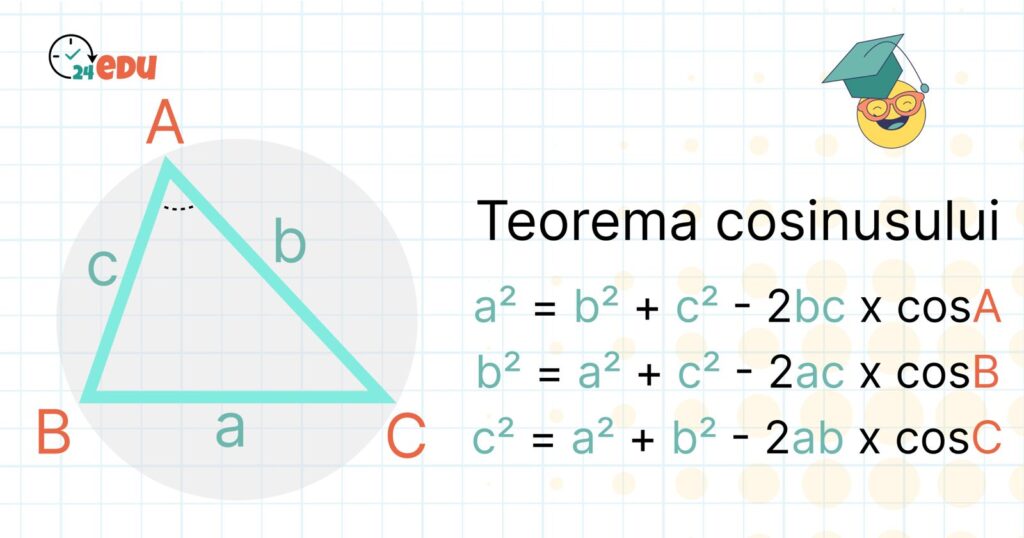
Imaginează-ți că ai un triunghi cu laturile a, b, c și unghiurile opuse acestora A, B, C.

a² = b² + c² – 2bc · cos A

b² = a² + c² – 2ac · cos B

c² = a² + b² – 2ab · cos C

În cazul în care avem un unghi de 90॰, cosinus de 90॰ este 0 și formula va fi teorema lui Pitagora, mai exact:

a² = b² + c²

Această teoremă este valabilă însă pentru orice triunghi, nu doar pentru cele dreptunghice.

Forma standard și explicarea fiecărui termen din teorema cosinusului

Formula standard a acestei teoreme este a² = b² + c² – 2bc · cos A, unde:

a este latura care se opune unghiului A și cea pe care vrem să o calculăm.
b și ce sunt laturile adiacente lui A.
cos A este cosinusul unghiului A, care leagă unghiul A de celelalte trei laturi ale triunghiului.

Exemple practice de aplicare a teoremei cosinusului

Teorema cosinusului, chiar dacă poate părea dificilă, în practică se poate aplica destul de simplu pentru mai multe situații, după cum urmează:

Măsurarea distanțelor care nu sunt accesibile

Dacă vrei de exemplu să măsori o distanță (A) dintre două puncte, B și C de pe un deal, dar nu poți, pentru că ai o râpă în față, teorema cosinusului te poate ajuta.

Ce ai de făcut este să măsori distanța de la punctul A la punctul B, apoi pe cea de la punctul A la punctul C. Unghiul care se va forma între acestea două este A. În acest caz, pentru a afla distanța dintre B și C calculăm: a² = b² + c² – 2bc · cos A.

Navigație

Și în navigație această teoremă este foarte utilă. Să presupunem că avem un avion care zboară dintr-un punct în două destinații diferite. Între direcțiile de zbor se va forma un unghi care ne va ajuta în aflarea distanței directe între cele două puncte.

Pentru a afla distanța dintre cele două puncte finale, cunoscând că traseul 1 are o lungime de 700 km și traseul 2 are o lungime de 800 km și unghiul format între ele este de 60॰, se va aplica teorema cosinusului.

a = 700 km;
b = 800 km;
C = 60 grade;
c = ?

Aplicăm teorema cosinusului: c² = a² + b² – 2ab · cos C și înlocuim cu datele pe care le cunoaștem:

c² = 700² + 800² – 2 · 700 · 800 cos · C (cos C = 60 grade = 0.5 – valoare standard)
c² = 1130000 – 550000
c² = 570000

Pentru a afla valoarea lui c, extragem rădăcina pătrată

c = 570000 ≈ 754.98 km.

Inginerie și construcții

Această teoremă poate fi utilă și în construcții. Inginerii o folosesc pentru a tăia corect materialele la acoperișuri sau diverse structuri triunghiulare.

Teorema cosinusului își găsește aplicații și în desing grafic și animație 3D, astronomie sau măsurători indirecte în arhitectură. Trebuie doar să o înțelegi puțin și să înveți să o aplici.

Cum demonstrezi teorema cosinusului pas cu pas

Pentru a demonstra teorema cosinusului avem nevoie de un triunghi oarecare, cu laturile ABC.

Notăm laturile triunghiului după cum urmează: BC = a, AC = b, AB = c. Unghiul care se formează între laturile b și c este unghiul A.

Din punctul C, construim o înălțime din vârful pe latura AB și anume CD, pe care o notăm cu h. Distanța de la A la D o notăm cu x, ceea ce înseamnă că DB va fi c – x.

Mai departe, cu ajutorul teoremei lui Pitagora exprimăm b și a, după cum urmează:

din triunghiul dreptunghic ADC: b² = h² + x² (1)
din triunghiul dreptunghic BDC: a² = h² + (c – x)² (2)

În continuare, înlocuim h² din enunțurile de mai sus și avem așa:

h² = b² – x²
a² = (b² – x²) + (c – x)²
a² = b² – x² + c² – 2cx + x²

Astfel observăm că – x² + x² = 0, ceea ce rezultă că: a² = b² + c² – 2cx (C)

Mai departe, folosind definiția cosinusului, aplicăm următoarele:

în triunghiul ABC, avem unghiul A care este între laturile b și c
în triunghiul ADC avem:

Ce ne mai rămâne de făcut este să înlocuim x în ecuația C, după cum urmează:

a² = b² + c² – 2c · (c · cos A)
a² = b² + c² – 2bc · cos A

Aplicații concrete în geometrie și trigonometrie a teoremei cosinusului

De-a lungul timpului, teorema cosinusului și-a dovedit utilitatea în geometrie și trigonometrie, mai exact, a fost aplicată cu succes în:

calcularea lungimilor laturilor unui triunghi oarecare, atunci când se cunoșteau deja două laturi și unghiul dintre ele;
determinarea mărimii unui unghi atunci când se cunosc lungimile tuturor laturilor dintr-un triunghi;
stabilirea naturii unghiurilor într-un triunghi;
calcularea ariei unui triunghi.

Ce diferențe sunt între teorema cosinusului și teorema lui Pitagora

Teorema cosinusului și cea a lui Pitagora sunt diferite, iar diferențele dintre ele țin de tipul triunghiului în care sunt aplicabile, dar și de prezența/absența unghiului în formulă.

Teorema lui Pitagora

Formula pentru teorema lui Pitagora este următoarea: a² = b² + c²

Această teoremă se aplică doar în cazul triunghiurilor dreptunghice, mai exact a celor care au un unghi de 90॰ care se formează între două laturi. În cadrul acestei teoreme nu se lucrează cu unghiuri.

Formula pentru teorema cosinusului este următoarea: a² = b² + c² – 2bc · cos A

Această teoremă se aplică la orice fel de triunghi, indiferent ce unghiuri formează, și are astfel o flexibilitate mult mai mare. Aceasta teoremă se reduce la teorema lui Pitagora când unghiul A este de 90॰, deoarece cos 90॰ = 0, ceea ce înseamnă că este egal cu a² = b² + c².

De ce este relevantă teorema cosinusului chiar și astăzi în epoca tehnologiei

Trăim într-o lume în care avem tehnologii moderne la fiecare pas, motiv pentru care, teorema cosinusului ar putea părea irelevantă. Însă, ea își păstrează relevanța și astăzi, deoarece stă la baza multor aplicații moderne, fiind întâlnită într-o mulțime de cazuri:

bază pentru algoritmi GPS și geolocalizare, unde trebuie determinată poziția prin triangulație, caz în care ajută la calculul distanțelor și unghiurilor în funcție de semnalele primite;
fundație pentru jocuri video, animații și aplicații grafice, deoarece permite calcularea de unghiuri între direcții, distanțe între puncte și colțuri de iluminare și umbre;
inteligență artificială, unde permite compararea de unghiuri și distanțe între puncte pe imagini sau corpuri atunci când vine vorba de recunoaștere facială sau diverse gesturi;
construcții și arhitectură, fiind utilă pentru proiectarea pieselor complexe, determinarea dimensiunilor în planuri neortogonale sau calculul forțelor și tensiunilor în structuri;
roboți și sisteme automate, unde ajută la formarea unghiurilor care contribuie la deplasarea dintr-un punct în altul.
astronomie și explorare spațială, deoarece ajută la calcularea traiectoriilor între planete, nave sau sateliți.

Sfaturi practice pentru rezolvarea corectă a exercițiilor cu teorema cosinusului

Exercițiile care implică folosirea teoremei cosinusului se pot dovedi a fi destul de dificile, motiv pentru care trebuie să te asiguri că faci totul pentru a avea rezultate cât mai precise. Pentru asta, vrem să îți venim în ajutor cu o serie de sfaturi:

fii atent atunci când identifici elementele triunghiului, deoarece este important să notezi clar fiecare latură, dar și unghiurile, și să cunoști bine formula pe care trebuie să o aplici. De regulă, cea mai mare eroare este cea în care se folosește un unghi care nu este cuprins între cele două laturi date.
folosește corect funcția cosinus, verificând atent aparatul cu care măsori unghiul, pentru a te asigura că este setat corect. Totodată, ai în vedere să nu rotunjești foarte mult rezultatul. Păstrează cel puțin 4 zecimale pentru o precizie cât mai bună.
alege forma potrivită a formulei pe care o folosești, în funcție de datele cunoscute în problema pe care o ai.
verifică și vezi dacă obții un rezultat logic atunci când calculezi un unghi. Ai în vedere că suma a două laturi trebuie să fie mai mare decât a treia.
pentru rezultate obținute cât mai simplu și corect, folosește-te și de desen. Desenează schematic triunghiul și vei găsi mult mai ușor ceea ce cauți.
fii atent la unitățile de măsură pe care le folosești și asigură-te de faptul că nu le încurci pe toată durata calculului.
folosește un calculator pentru a calcula cu ușurință cosinusuri, extrageri de rădăcini și alte date importante.
pentru a fi totul cât mai corect și mai simplu de urmărit, scrie toate etapele pe care le parcurgi.

Aceste sfaturi sunt foarte utile atât elevilor, cât și celor care din diverse motive trebuie să lucreze cu astfel de calcule matematice care sunt ceva mai complexe.

Cum să aprofundezi mai mult și să devii expert în aplicarea teoremei cosinusului

Dacă vrei să aprofundezi teorema cosinusului și nu știi exact cum poți face asta, află că sunt o serie de aspecte simple pe care le poți pune în practică:

începe cu aprofundarea și înțelegerea conceptelor de bază precum: triunghi oarecare, cosinus, unghi, laturi etc. Astfel vei ști exact despre ce se vorbește și vei înțelege mai ușor.
caută să rezolvi probleme în mod progresiv, mai exact începând de la cele mai simple, apoi avansând. Poți începe cu exerciții în carese știu două laturi și un unghi, apoi să avansezi la cele care au specificate doar laturile și trebuie să afli unghiurile și apoi la probleme de geometrie aplicată.
învață prin vizualizare, făcând tot felul de schițe sau utilizând programe interactive pe care le poți descărca de pe platformele online.
aplică în viața reală teorema cosinusului, inventând tot felul de probleme legate de distanțe între anumite puncte, unghiuri, măsurarea poziției etc.

Învățând în mod constant și aprofundând totul într-un mod cât mai practic, vei vedea că teorema cosinusului nu este atât de dificilă precum ar putea să pară la o primă vedere.

Teorema cosinusului – Formula și definiție