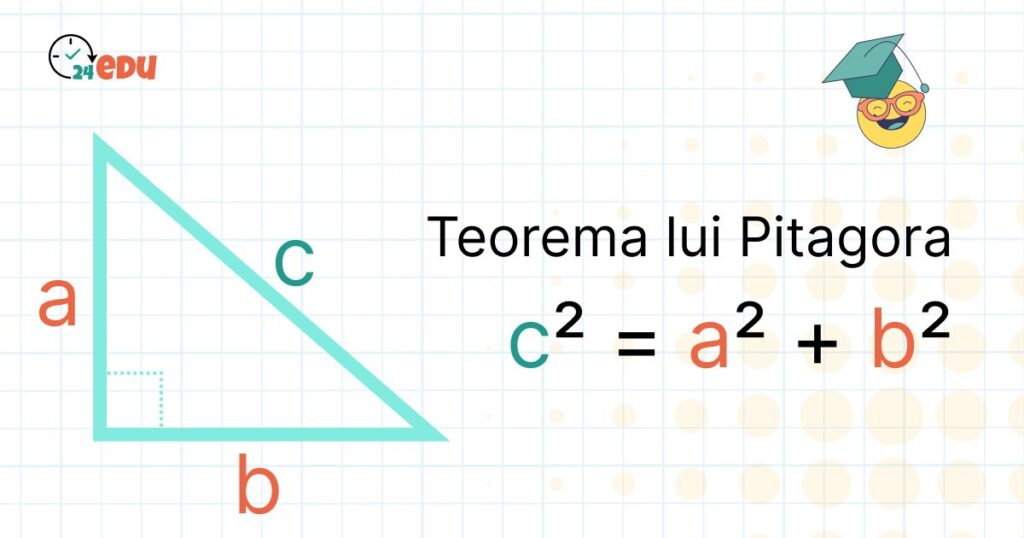
Triunghiurile reprezintă una dintre cele mai simple și studiate forme geometrice. Dintre toate tipurile de triunghiuri, triunghiul dreptunghic ocupă un loc special datorită proprietăților sale unice și aplicațiilor variate.
Un triunghi dreptunghic este un triunghi care are un unghi de 90°. Cele trei laturi ale acestuia poartă denumiri specifice:
- Catetele sunt cele două laturi care formează unghiul drept.
- Ipoteuza este latura opusă unghiului drept și este, întotdeauna, cea mai lungă dintre cele trei.
Aceste elemente formează baza pe care se construiește teorema lui Pitagora – o relație fundamentală în geometrie care leagă lungimile celor trei laturi ale unui triunghi dreptunghic.
Înainte de a învăța formula, este important să înțelegem clar cum arată un triunghi dreptunghic și să putem identifica ipotenuza și catetele în orice desen geometric. Aceste noțiuni vor fi esențiale pentru aplicarea corectă a teoremei lui Pitagora în problemele matematice.
Pitagora – viața și contribuțiile unui gânditor remarcabil
Pitagora a fost un filosof și matematician grec, născut în jurul anului 570 î.Hr. în insula Samos. Deși este cunoscut în special pentru teorema care îi poartă numele, influența sa se extinde mult dincolo de domeniul matematicii. A călătorit în tinerețe în Egipt, Babilon și poate chiar în India, unde a studiat științele, religia și filosofia acelor civilizații. Ulterior, s-a stabilit în sudul Italiei, în Crotona, unde a fondat o comunitate filosofică și religioasă – școala pitagoreică.
Această școală era mai mult decât un loc de învățare: era o comunitate cu reguli stricte, bazate pe autocontrol, tăcere, respect și cercetare științifică. Membrii erau împărțiți în „acuzmatici” (ascultători) și „matematicieni” (cei inițiați în învățăturile mai profunde). Pitagoreicii considerau că întreaga realitate poate fi explicată prin numere și proporții, iar această idee a pus bazele unei noi abordări în gândirea științifică.
În matematică, Pitagora este cel mai faimos pentru enunțarea relației dintre laturile unui triunghi dreptunghic: suma pătratelor catetelor este egală cu pătratul ipotenuzei. Deși această teoremă era cunoscută și utilizată în Babilon cu mult înainte, Pitagora sau adepții săi au fost primii care au oferit o demonstrație riguroasă.
Pitagora a avut un impact major și în muzică, descoperind legătura dintre lungimea corzilor și notele muzicale, punând astfel bazele acusticii. De asemenea, a fost preocupat de etică, cosmologie și armonia universului, văzută prin prisma proporțiilor matematice.
Pitagora rămâne una dintre figurile centrale ale Antichității, influențând profund nu doar matematica, ci și modul în care înțelegem lumea.
Definiția teoremei lui Pitagora
Conform CueMath, teorema lui Pitagora este una dintre cele mai cunoscute și fundamentale teoreme din geometrie. Ea se aplică doar în cazul triunghiurilor dreptunghice și exprimă o relație între cele trei laturi ale triunghiului.
Enunțul teoremei este următorul:
Într-un triunghi dreptunghic, pătratul ipotenuzei este egal cu suma pătratelor catetelor.
Această relație poate fi exprimată matematic prin formula:
a² + b² = c²
unde:
- a și b sunt lungimile catetelor
- c este lungimea ipotenuzei
Teorema poartă numele filosofului și matematicianului grec Pitagora, care a trăit în secolul al VI-lea î.Hr., deși se crede că relația era cunoscută și aplicată încă dinaintea vremii sale, în diverse civilizații antice.
Această formulă este esențială nu doar în geometrie, ci și în alte domenii precum fizica, arhitectura, informatica sau navigația, datorită simplității și eficienței cu care permite calcularea distanțelor.
Formula teoremei lui Pitagora
După ce am înțeles definiția teoremei, putem pune accentul pe modul concret în care se aplică formula pentru a rezolva probleme.
Formula de bază este:
a² + b² = c²
unde:
- a și b reprezintă lungimile catetelor
- c este lungimea ipotenuzei (latura opusă unghiului de 90°)
Această formulă se folosește în două moduri principale:
- Pentru a calcula ipotenuza atunci când se cunosc cele două catete:
c = √(a² + b²) - Pentru a calcula o catetă atunci când se cunoaște ipotenuza și cealaltă catetă:
a = √(c² – b²) sau b = √(c² – a²)
Este important ca această formulă să fie aplicată doar în triunghiuri dreptunghice, altfel rezultatele vor fi incorecte.
Formula este simplă, dar extrem de puternică, fiind folosită frecvent pentru a rezolva probleme legate de distanțe, înălțimi, diagonale sau trasee în spațiu.
Demonstrarea teoremei lui Pitagora
De-a lungul timpului, teorema lui Pitagora a fost demonstrată în peste 300 de moduri diferite. Unele sunt geometrice, altele algebrice, iar altele chiar vizuale. Vom prezenta o demonstrație geometrică simplă și intuitivă, potrivită pentru înțelegerea de bază a relației dintre laturile unui triunghi dreptunghic.
Pasul 1: construirea unui pătrat mare
Se construiește un pătrat cu latura de (a + b), în interiorul căruia se inserează 4 triunghiuri dreptunghice identice, fiecare cu catetele a și b, și ipotenuza c.
Pasul 2: observarea spațiului rămas
După ce cele 4 triunghiuri sunt așezate în colțurile pătratului mare, în mijloc rămâne un pătrat mic, ale cărui laturi au lungimea c (ipotenuza fiecărui triunghi).
Pasul 3: calcularea ariei în două moduri
- Prima metodă: Aria pătratului mare este
(a + b)² = a² + 2ab + b² - A doua metodă: Aria totală este formată din aria celor 4 triunghiuri și aria pătratului mic din centru:
4 × (ab / 2) + c² = 2ab + c²
Pasul 4: egalarea celor două expresii
Se egalizează cele două variante de calcul:
a² + 2ab + b² = 2ab + c²
Scăzând 2ab de ambele părți:
a² + b² = c²
Aplicații ale teoremei în viața reală
Deși pare o formulă simplă, teorema lui Pitagora are o mulțime de utilizări practice, dincolo de paginile cărților de matematică. Oriunde există distanțe, unghiuri drepte sau forme geometrice, teorema își găsește locul.
- Calculul distanței directe între două puncte
Când nu poți merge în linie dreaptă, dar cunoști distanțele pe orizontală și pe verticală, poți folosi teorema pentru a afla cât de departe sunt două puncte. - Construcții și arhitectură
Pentru a verifica dacă un colț este drept (90°) sau pentru a măsura diagonala unui perete sau a unei plăci, constructorii folosesc frecvent teorema. - Navigație și orientare GPS
Pentru a calcula distanța cea mai scurtă între două locații pe o hartă (într-un plan bidimensional), se folosește adesea relația dintre coordonate bazată pe teorema lui Pitagora. - Calculul diagonalei unui dreptunghi sau pătrat
De exemplu, dacă vrei să afli dacă un televizor încape pe un perete, teorema te ajută să calculezi diagonala ecranului sau a spațiului disponibil. - Inginerie și robotică
În mișcările brațelor robotice sau în proiectarea de trasee, se folosește teorema pentru a determina poziționarea corectă în spațiu. - Arte vizuale și design grafic
Pentru a construi perspective corecte, proporții sau pentru a reda adâncimea într-o imagine, se aplică frecvent concepte bazate pe această teoremă.
Această versatilitate face ca teorema lui Pitagora să fie nu doar o lecție de matematică, ci și un instrument de zi cu zi în multe meserii și domenii.
Exemple de probleme rezolvate
Pentru a înțelege mai bine cum se aplică teorema lui Pitagora, vom analiza câteva probleme simple, pas cu pas.
Exemplul 1: Calculul ipotenuzei
Enunț:
Un triunghi dreptunghic are catetele de 3 cm și 4 cm. Care este lungimea ipotenuzei?
Soluție:
Aplicăm formula teoremei lui Pitagora:
a² + b² = c²
3² + 4² = c²
9 + 16 = c²
25 = c²
c = √25 = 5 cm
Exemplul 2: Calculul unei catete
Enunț:
Într-un triunghi dreptunghic, ipotenuza are 13 cm, iar una dintre catete are 5 cm. Ce lungime are cealaltă catetă?
Soluție:
Folosim formula inversă:
a = √(c² – b²)
a = √(13² – 5²) = √(169 – 25) = √144 = 12 cm
Exemplul 3: Diagonala unui dreptunghi
Enunț:
Un dreptunghi are laturile de 6 m și 8 m. Care este lungimea diagonalei?
Soluție:
Diagonala formează un triunghi dreptunghic cu laturile dreptunghiului.
Folosim teorema lui Pitagora:
d² = 6² + 8² = 36 + 64 = 100
d = √100 = 10 m
Exemplul 4: Verificarea dacă un triunghi este dreptunghic
Enunț:
Un triunghi are laturile de 7 cm, 24 cm și 25 cm. Este un triunghi dreptunghic?
Soluție:
Verificăm dacă se respectă a² + b² = c²
7² + 24² = 49 + 576 = 625
25² = 625
Pentru că 625 = 625, triunghiul este dreptunghic.
Exerciții propuse pentru exersare
Exerciții propuse pentru exersare
1. Calculează ipotenuza unui triunghi dreptunghic care are catetele de 6 cm și 8 cm.
2. Un triunghi dreptunghic are ipotenuza de 10 cm și o catetă de 6 cm. Află cealaltă catetă.
3. Un dreptunghi are laturile de 9 m și 12 m. Determină lungimea diagonalei.
4. Un triunghi are laturile de 9 cm, 12 cm și 15 cm. Verifică dacă este un triunghi dreptunghic.
5. Într-un triunghi dreptunghic, ipotenuza măsoară 17 cm, iar una dintre catete 15 cm. Calculează lungimea celeilalte catete.
6. O scară lungă de 5 m este sprijinită de un perete vertical, iar baza scării se află la 3 m de perete. Cât de sus urcă scara pe perete?
7. Un pătrat are latura de 7 cm. Află lungimea diagonalei.
8. Un teren de sport are forma unui dreptunghi cu laturile de 20 m și 21 m. Calculează diagonala pentru a verifica dacă este corect trasat.
Greșeli frecvente și cum să le eviți
Chiar dacă teorema lui Pitagora este simplă ca formulă, apar adesea greșeli în aplicarea ei, mai ales în rezolvarea exercițiilor:
- Aplicarea teoremei în triunghiuri care nu sunt dreptunghice
Greșeală: folosirea formulei a2+b2=c2a² + b² = c²a2+b2=c2 într-un triunghi oarecare.
Cum o eviți: verifică întotdeauna dacă triunghiul are un unghi drept (90°) înainte de a aplica teorema.
- Identificarea greșită a ipotenuzei
Greșeală: considerarea oricărei laturi ca fiind ipotenuza.
Cum o eviți: ipotenuza este întotdeauna latura opusă unghiului drept și cea mai lungă latură din triunghi.
- Calcul greșit al rădăcinii pătrate
Greșeală: extragerea greșită a rădăcinii pătrate sau uitarea acesteia.
Cum o eviți: după ce obții c2c²c2, nu uita să aplici corect rădăcina pătrată: c=√(a2+b2)c = √(a² + b²)c=√(a2+b2)
- Inversarea catetelor cu ipotenuza în formula
Greșeală: scrierea formulei greșite, de tipul c2+a2=b2c² + a² = b²c2+a2=b2.
Cum o eviți: memorează clar ordinea corectă: suma pătratelor catetelor = pătratul ipotenuzei
- Lipsa unităților de măsură în răspunsuri
Greșeală: oferirea unui rezultat fără unitate (ex: “răspunsul este 10”).
Cum o eviți: adaugă mereu unitatea de măsură în final (cm, m, etc.), în funcție de datele din problemă.
- Rotunjiri premature sau incorecte
Greșeală: rotunjirea valorii înainte de a termina calculele.
Cum o eviți: rotunjește doar la final, și menționează dacă ai aproximat (ex: „aproximativ 7,1 cm”).
Legătura dintre teorema lui Pitagora și alte concepte matematice
Teorema lui Pitagora nu este izolată de restul matematicii – dimpotrivă, ea este strâns legată de multe alte concepte importante, care apar atât în gimnaziu, cât și în liceu.
Geometria în spațiu (3D)
Extinderea teoremei în 3 dimensiuni permite calcularea distanței între două puncte în spațiu. De exemplu, pentru un paralelipiped dreptunghic, diagonala sa se calculează cu o formulă derivată din teorema lui Pitagora:
d = √(l² + L² + h²)
Distanta dintre două puncte într-un plan
Formula distanței dintre două puncte cu coordonate (x1,y1)(x₁, y₁)(x1,y1) și (x2,y2)(x₂, y₂)(x2,y2) este:
d = √[(x₂ – x₁)² + (y₂ – y₁)²]
Aceasta este, practic, o aplicare directă a teoremei lui Pitagora în sistemul de coordonate cartezian.
Trigonometria
Funcțiile trigonometrice – sinus, cosinus și tangenta – se bazează pe relațiile din triunghiul dreptunghic. Teorema lui Pitagora este esențială pentru deducerea formulelor trigonometrice fundamentale.
Cerc și geometrie analitică
Ecuația unui cerc cu centrul în origine și rază rrr este:
x² + y² = r²
Aceasta derivă din teorema lui Pitagora, considerând distanța de la un punct (x,y)(x, y)(x,y) până la origine.
Teorema reciproca a lui Pitagora
Această teoremă afirmă că dacă într-un triunghi suma pătratelor a două laturi este egală cu pătratul celei de-a treia, atunci acel triunghi este dreptunghic. Este folosită frecvent pentru verificarea unui triunghi.
Teorema catetei și teorema înălțimii
Acestea sunt teoreme derivate, care completează înțelegerea relațiilor dintre elementele unui triunghi dreptunghic. De exemplu:
Cateta² = proiecția ei pe ipotenuză × ipotenuza
Teorema lui Pitagora reprezintă una dintre cele mai importante relații din geometrie, datorită simplității și aplicabilității sale în numeroase situații. Ea leagă în mod elegant laturile unui triunghi dreptunghic și devine un instrument esențial în rezolvarea problemelor care implică distanțe, diagonale sau unghiuri drepte. Prin înțelegerea și stăpânirea acestei teoreme, se creează o bază solidă nu doar pentru studiul geometriei, ci și pentru ramuri mai complexe ale matematicii, fizicii sau informaticii.

Leave a Reply