În matematică, mai exact în geometria triunghiurilor, teorema sinusurilor este extrem de importantă atunci când lucrăm cu triunghiuri care nu sunt dreptunghice. Aceasta este utilă în rezolvarea unor probleme complexe, fiind o formulă simplă ce leagă laturile și unghiurile unui triunghi.
Pentru orice elev care vrea să învețe geometrie plană este foarte important să înțeleagă în mod corect această teoremă, mai exact să priceapă condițiile în care se aplică și modul în care se folosește.
Ce este sinusul
Înainte de a trece la teorema sinusului, vrem să îți vorbim puțin despre ce este sinusul unui unghi, pentru a înțelege totul mult mai ușor.
Sinusul unui unghi reprezintă o funcție trigonometrică importantă, care leagă un unghi de raportul dintre două laturi, într-un triunghi dreptunghic.
Pentru asta, avem și o formulă care spune că:
sin A = cateta opusă unghiului Aipotenuză
Dacă, de exemplu, avem un triunghi dreptunghic cu următoarele date:
- unghi A de 30 de grade;
- cateta opusă unghiului A = 5 cm;
- ipotenuza = 10 cm.
Aplicând formula obținem:
sin 30° = 510 = 0.5
Sinusul unui unghi nu este o lungime, ci un raport, iar valorile lui sunt între 0 și 1. Aceste valori sunt unele pe care le ai deja calculate și le regăsești în tabele precum acesta de pe Wikipedia.
Dacă este vorba de triunghiuri care nu au un unghi de 90 de grade, sinusul va fi definit cu ajutorul unui cerc trigonometric, așa cum se întâmplă în cazul teoremei sinusurilor.
Ce este teorema sinusului și cum poate fi demonstrată
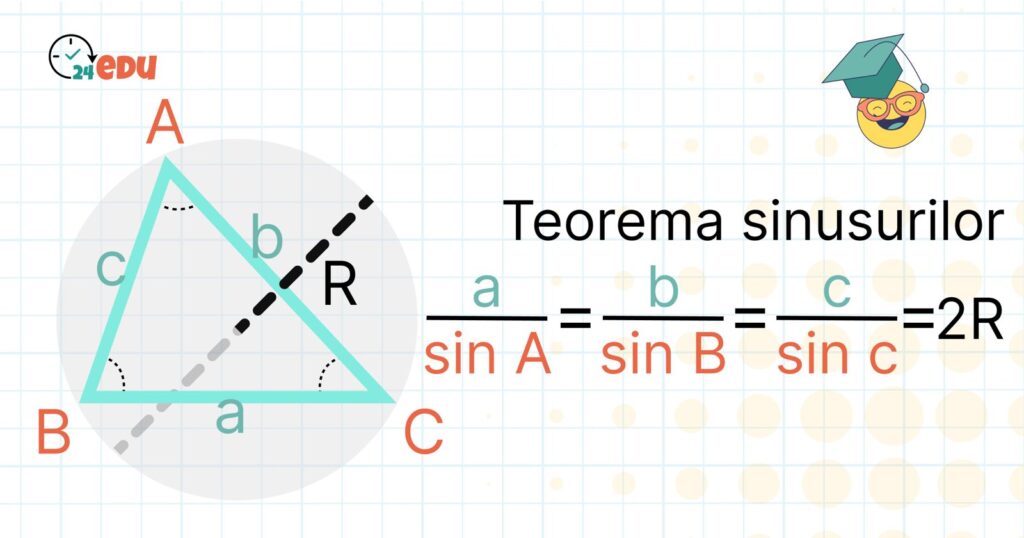
O relație fundamentală în geometria triunghiurilor este reprezentată de teorema sinusurilor, care stabilește relația dintre valorile laturilor unui triunghi și sinusurile unghiurilor dintre ele.
Pentru a exemplifica acest lucru, se dă un triunghi oarecare cu laturile a, b, c și unghiurile opuse acestora A, B, C și se obține următoarea relație, conform GeoGebra:
- a, b, c = laturile triunghiului;
- A, B, C – unghiurile opuse laturilor triunghiului;
- R = raza cercului circumscris triunghiului.
Totodată, trebuie să știm, așa cum ne învață manualele de matematică, faptul că în orice triunghi, raportul dintre o latură și sinusul unghiului opus este constant și egal cu diametrul cercului circumscris triunghiului.
Acestea fiind zise, din teorema sinusului rezultă următoarele:
- a = 2R sin A;
- b = 2R sin B;
- c = 2R sin C.
Pentru a demonstra acest lucru, avem nevoie de un cerc circumscris unui triunghi ascuțitunghic ABC.
- BD = diametrul cercului;
- ∆ BCD este dreptunghic în C, iar ∢ BAC = ∢ BDC
- prin urmare: sin ∢ BAC = ∢ BDC = BCBD = a2R
- din aceasta rezultă că:
- sin B = b2R
- sin C = c2R
Sursa: Algebra and Trigonometry: Functions and Applications, Paul A. Foerster
Formula teoremei sinusului explicată simplu și logic
Dacă ceea ce am prezentat mai sus te-a băgat puțin în ceață, vom încerca să îți mai explicăm încă o dată această teoremă, în termeni mai simpli.
Teorema sinusului ne învață următoarele:
- în orice triunghi raportul dintre lungimea unei laturi și sinusul unghiului opus este egală cu același raport și pentru celelalte două laturi;
- relația aceasta este una care se aplică în orice tip de triunghi – ascutitunghic, dreptunghic, obtuzunghic;
- dacă ai date cu privire la un unghi și latura lui opusă, poți să afli alte unghiuri și laturi pentru care nu ai date în enunț.
Această teoremă este foarte utilă atunci când nu putem folosi teorema lui Pitagora, deoarece nu există un unghi drept.
La ce folosește teorema sinusurilor în matematică
În matematică, avem nevoie de teorema sinusurilor pentru a rezolva probleme cu triunghiuri care nu sunt dreptunghice, ci ascutitunghice și obtuzunghice.
Mai exact, dacă știm valoarea unui unghi, dar și latura lui opusă, dar și un alt unghi sau o altă latură, putem afla valoarea altor laturi pe care nu le cunoaștem.
Totodată, dacă știm două laturi și un unghi, putem să aflăm valoarea unui alt unghi, toate acestea cu ajutorul formulei:
asin A = bsin B ⇒ b = a · sin Bsin A
În matematică, teorema sinusurilor poate ajuta și la determinarea razei cercului care trece prin toate vârfurile unui triunghi, cu ajutorul formulei:
asin A = 2R ⇒ a2 sin A
La ce folosește teorema sinusurilor în viața reală
Orice teoremă din matematică este folositoare în viața reală, chiar dacă de multe ori nu realizăm acest lucru. La fel se întâmplă și cu teorema sinusurilor, pe care o putem întâlni în:
- topografie și măsurători pe teren
Teorema sinusurilor permite calcularea distanței folosind unghiuri și distanțe ușor de măsurat de pe margine, motiv pentru care vine în ajutorul inginerilor atunci când trebuie să măsoare distanțe între puncte aflate în zone greu accesibile, ca de exemplu, de-o parte și de alta a unui râu sau în zone muntoase.
- navigație maritimă și aeriană
Teorema sinusurilor este folosită de specialiștii din aceste domenii când stabilesc rute între două puncte de pe glob, unghiurile și distanțele dintre puncte care sunt calculate ținând cont de curbura Pământului.
- astronomie
Astronomii folosesc teorema sinusurilor pentru a calcula distanțele până la stele sau alte corpuri cerești. De exemplu, prin metoda paralaxei (observând un obiect ceresc din două puncte diferite ale orbitei Pământului), se formează un triunghi, iar distanța necunoscută poate fi determinată.
- inginerie și arhitectură
Inginerii din aceste domenii folosesc teorema sinusurilor în proiectarea structurilor care nu sunt dreptunghiulare (acoperișuri înclinate, grinzi oblice, susținători). Astfel, ei reușesc să obțină stabilirea dimensiunilor corecte fără măsurători directe.
- construcții și design interior
Teorema Sinusurilor poate fi folosită și în construcții și design interior, pentru a determina ce formă sau lungime trebuie să aibă o piesă. De exemplu, în amenajări interioare sau lucrări de tăiere a materialelor la unghiuri specifice ea poate fi foarte utilă.
- tehnologie și robotică
Teorema Sinusurilor este esențială în tehnologie și robotică, pentru determinarea poziției finale a unui punct în funcție de unghiuri și lungimi date. Este întâlnită în simularea mișcării brațelor mecanice, dar și în unghiurile și lungimile segmentelor care trebuie calculate precis.
Diferențe esențiale între teorema sinusului și teorema cosinusului
În geometria triunghiului întâlnim frecvent două teoreme: cea a sinusului și cea a cosinusului. Acestea sunt diferite și se aplică în contexte diferite, motiv pentru care este bine să le studiezi puțin prin comparație, pentru a-ți da seama când, unde și cum se aplică.
- în funcție de cazurile în care se aplică
- teorema sinusului se aplică în triunghiurile ascutitunghice și obtuzunghice, când cunoști un unghi și latura opusă;
- teorema cosinusului se aplică în orice triunghi, când cunoști două laturi și unghiurile dintre ele sau trei laturi:
- formula de calcul
- formula de calcul folosită în teorema sinusului este:
asin A = bsin B = csin C
- formula de calcul folosită în teorema cosinusului este:
a² = b² + c² – 2bc · cos A
- dificultatea de aplicare
- teorema sinusului este cea mai ușor de aplicat, deoarece se bazează pe rapoarte clare și reguli simple;
- teorema cosinusului este ceva mai dificilă, mai complexă, implicând mai multe calcule algebrice.
- riscul de ambiguitate
- teorema sinusului poate fi uneori ambiguă, mai ales când se dovedește că nu există nici un triunghi valid;
- teorema cosinusului este mai sigură în cazurile mai complexe și oferă rezultate unice.
Când și cum aplicăm teorema sinusului în probleme
Este important să știi când și cum aplici teorema sinusului în problemele de matematică, pentru a obține rezultate corecte.
Această teoremă, așa cum am mai spus, se aplică doar în triunghiuri ascuțitunghice, obtuzunghice sau echilaterale, în următoarele cazuri:
- ULU – când cunoaștem două unghiuri și o latură;
- LUU – când cunoaștem o latură și două unghiuri;
- LUL – când cunoaștem două laturi și un unghi.
Pentru a aplica această teoremă sunt necesari următorii pași:
- se identifică perechea ULU, LUU sau LUL;
- se aplică formula de calcul asin A = bsin B = csin C
Pentru a înțelege mai bine iată un exemplu concret:
- avem triunghiul ABC;
- ∢ A = 40°;
- ∢ B = 60°;
- a = 10 cm.
Calculăm cât este unghiul C, pornind de la faptul că într-un triungi suma unghiurilor trebuie să fie de 180°.
C = 180° – A – B = 180° – 40° – 60° = 80°.
Mai departe, aplicăm teorema sinusului:
asin A = csin C ⇒ 10sin 40° = csin 80°
c = 10 · sin 80°sin 40° ≈ 10 · 0.9848 0.6428 ≈ 15.33 cm.
Cele mai frecvente greșeli ale elevilor și cum le poți evita
La o primă vedere poate părea simplu să aplici această teoremă, mai ales dacă ai înțeles exact ce am discutat până acum. Și într-adevăr este simplu, dar, rezolvarea exercițiilor simple de multe ori poate deveni inexactă, deoarece se încurcă ușor diverse formule, calcule etc.
Pentru a te asigura că vei ajunge la un rezultat cât mai exact, ai în vedere evitarea următoarelor greșeli:
- confundarea unghiurilor cu laturile opuse
Ai grijă ca în aplicarea formulei aferente teoremei sinusului să respecți cu precizie perechea latură – unghi opus. Fiecare latură va fi în raport cu unghiul opus, mai exact nu folosești asin B, bsin c sau csin A, ci asin A, bsin B și csin C
- folosirea în mod greșit a calculatorului
Calculele în teorema sinusurilor implică uneori și utilizarea unui calculator. Unii elevi nu sunt atenți la modul în care este setat respectivul dispozitiv și ajung astfel la rezultate eronate. Cel mai frecvent asta se întâmplă când calculatorul este setat pe radiani, nu pe grade.
- lipsa aplicării funcției inverse la calcularea unghiurilor
În cazul în care ceea ce trebuie să afli este valoarea unui unghi, ai în vedere faptul că se aplică funcția inversă, și anume arcsin. Mai exact, dacă ai sin A = 0.5, unghiul A va fi sin-1 (0.5) = 30 grade.
- aplicarea teoremei unde nu este cazul
Când dorești să aplici teorema sinusurilor, asigură-te că ai datele necesare pentru a vedea acest lucru, mai exact că din enunț se înțelege clar sau se deduce una dintre perechile: ULU, LUU sau LUL.
- neverificarea rezultatelor obținute
După ce ai făcut calculele necesare și ai obținut rezultatul final, ce mai poți face mai departe este să verifici dacă ai aplicat formulele corect și ai făcut calculele corecte.
Cel mai ușor poți face asta calculând suma totală a unghiurilor, care trebuie să fie de 180 de grade, dar și inegalitatea laturilor în triunghi, mai exact dacă orice latură este mai mică decât suma celorlalte două.
Verifică-ți cunoștințele
Haide să vedem dacă ai înțeles cele prezentate în acest text, răspunzând la următoarele întrebări:
1. Ce reprezintă „sin A” într-un triunghi?
a. Lungimea unghiului A
b. Valoarea numerică a unghiului A în radiani
c. Raportul dintre cateta opusă și ipotenuză (sau valoarea funcției sinus a unghiului A)
c. Produsul dintre latura a și unghiul A
2. În ce tip de triunghiuri se aplică teorema sinusului?
a. Doar în triunghiuri dreptunghice
b. Doar în triunghiuri echilaterale
c. În orice triunghi, dar mai ales în triunghiuri oblice
d. Doar în triunghiuri isoscele
3. Scrie formula teoremei sinusului
4. Poți folosi Teorema Sinusului dacă ai trei laturi și nici un unghi cunoscut?
a. Da, întotdeauna
b. Nu, ai nevoie de cel puțin o pereche latură–unghi opus
c. Da, dar doar dacă laturile sunt egale
d. Numai dacă triunghiul este dreptunghic
5. Dacă a = 10 cm, A = 30 grade, cât este asin A?
a. 5
b. 10
c. 20
d. 30
6. Care este condiția minimă pentru a aplica corect teorema sinusurilor?
a. Să știi măcar două unghiuri
b. Să cunoști o pereche latură–unghi opus
c. Să ai toate cele trei laturi
d. Să știi măcar un unghi drept
7. Ce se întâmplă dacă folosești unghiul adiacent în locul celui opus în formulă?
a. Formula se aplică normal
b. Rezultatul este mai rapid
c. Obții rezultate greșite
d. Se simplifică formula
8. De ce trebuie folosită funcția „arcsin” în unele probleme?
a. Pentru a calcula lungimea laturii
b. Pentru a obține valoarea unui unghi dintr-un sinus cunoscut
c. Pentru a calcula aria triunghiului
d. Pentru a verifica dacă triunghiul este isoscel
Răspunsuri:
1. C
2. C
3. asin A = bsin B = csin C
4. B
5. C
6. B
7. C
8. B
Așa după cum bine ți-ai dat seama din cele specificate în acest text, teorema sinusului este un instrument matematic foarte valoros, care face legătura dintre unghiurile și laturile unui triunghi oblic.
Dacă ai înțeles-o și o vei aplica corect, vei reuși să eviți o mulțime de greșeli în problemele matematice și vei obține la final rezultate corecte și concludente.

Leave a Reply